プロコン
プロコンサイト †
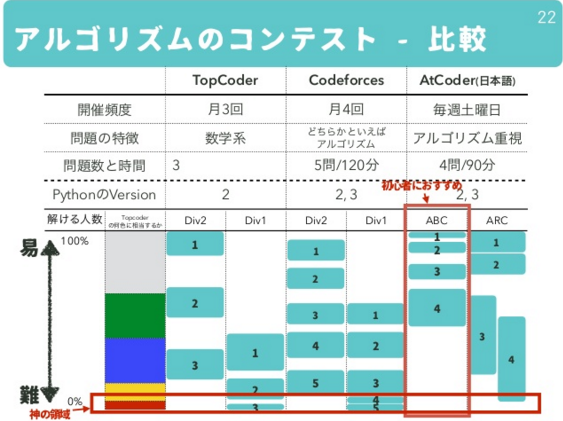
Topcoder †
- 難易度はD1E<<D2M<=D1E<D1H<=D1M<D1H
- 例えばLuckySum?はDiv1 EasyがDiv2 Hard
- Challenge
- vectorのチャレンジの仕方
hoge,foo,test
- とすると、vector[3]={hoge, foo, test};となる。変なスペースはつけてはならない、最後にカンマをつけてはならない。
- Topcoderはやたら制約が雑
- 大体の制約がN<50
- n!、2^n, nCn/2の全探索は無理。
- 2^25の半分全列挙はできる。
Codeforces †
Atcoder †
- 日本語、解説が付いているのが良い。
- 他の人のコードを気軽にコピーできるので比較もしやすい。
csac academy †
問題の見方 †
流れ †
- google翻訳に問題文を突っ込む
- 実験
- 明らかな条件を列挙し、覚えておく。自明な条件をコーナーケースとして把握する。
- 求められる情報量の確認
- yes-noか、max-minか、numかなど。少ない情報ならまとめられる。
- 計算機特有の発想
- 特性関数の作りやすさ。この答え(以上・以下)は問いの答えたりえるか?という質問に簡単に答えられるかを確認する。
- 半分全列挙。問題を半分にすると、マージが楽ではないか?
- DP。問題を極限まで小さくしたら、自明な解が存在しないか?そして、小さい問題から大きい問題の答えにできないか?
- ダブリング。半分半分の漸化式が作れるか?
- 計算量
- アルゴリズムに要求される計算量のキツさを確認する。
- 頑張って実装
- テスト
- 時間最大セットと、メモリ最大セットと、コーナーケースで通るかを確認する。
- 疎な最大ケース 1 100000000
- 密な最大ケース 10000000000 1000000000
- 疎密ケース 1 1 1 1 1 100000 100000 100000 1000000 100000 1 1 1 1 1
チェックリスト †
| チェック項目 | 説明 | | デバッグメッセージを残すな | | | 自前テストしたか | 極端な例(入力の小さいもの大きいもの)、最小の普通なもの、普通なもの、疎密(密粗密なども) | | 1行に複数の値を返す時、きちんと最後のスペースを除け | | | コーナーケースできちんとcout << 1 << endl; return 0;せよ | Atcoder, Codeforcesなどだと、間違えてreturn ret;とかすると死ぬ | | intを全てlong longにせよ | 掛け算でキャストミスしないために | | 数字リテラルをlong long, long doubleにせよ | 掛け算とbit shiftでキャストミスしないように。1ll, 1.0l | | INF, EPSを使っているなら、その値は正しいか | INF大きすぎると、INF+aでオーバーフローしかねない。 | | はじめに書いたコーナーケースを最後にも確認せよ | | | 整数同士の掛け算がオーバーフローしないか確認せよ | 10^18とかの場合、一回も掛け算してはならない!c[i]*c[i+1]でオーバーフローしえるので注意。 | | 整数同士の割り算がlgaussかugaussか確認 | intがlgaussになるのは同符号の時だけ | | valgrindをかけよ | | | 盤面問題で、添字はあっているか確認せよ | 添字のn, mを逆にしたりしてないか? | | 負の%とif文が同時にないか確認 | 両方正にして比較すること | | Mod構造体のリテラルは必ずキャストすること | ^がxorと判断されたりなど超絶面倒なバグが起きる |
コーディング注意 †
| 注意点 | 説明 | | 盤面など添字が複雑な場合は、なるべく命名規則を一貫させること | (i, j)の盤面の大きさはni, njなど |
入出力 †
- cinは遅い。
- 30万変数読み込みで、scanfだと50ms, cinだと150ms
- 同期を切ると早くなる
- 切ったらもうcinとscanfを混ぜて使ってはいけない
計算量 †
| 計算量 | 安全 | 無理 | | O(n) | 3000万 | 1億=10^8 | | O(n log n) | 100万 | 400万 | | O(n^2) | 5000 | 10000 | | O(n^3) | 300 | 450 | | O(n^4) | 75 | 100 | | O(2^n) | 25 | 27 | | O(3^n) | 15 | 17 |
- 制約2秒程度だったら、逆にどんな計算量が求められている?
| 制約 | アルゴリズム | | 10^6 | O(n)以下、軽いO(n log n) | | 10^5 | O(n log n)以下 | | 3000 | O(n^2) | | 500 | 軽いO(n^3) | | 100 | O(n^3) | | 30 | O(2^n)の半分全列挙 | | 20 | O(2^n)、O(n 2^n) |
- 違い
- ならし計算量 : 時系列上での平均
- 平均計算量 : 確率変数上での平均
よく使うデータ構造と関数と注意点早見表 †
| 名前 | メソッド | 注意 | | unordered_map | erase, count, find | tupleを突っ込めない。ソートされない。でも速い。 | | map | erase, count, find | tupleを突っ込める。50000要素でunordered_mapの3倍遅い。比較1, 2, m.findはnot foundでm.end(), その他でイテレータを返す | | set | count, erase, insert | | | queue | empty, size, front, pop, push | | | priority_queue | empty, size, top, pop, push | デフォルトで降順 | | stack | empty, size, top, pop, push | | | deque | push_back, push_front | 前に挿入できるvector。前に挿入できるので添字が移動する | | vector | push_back | vector<bool>は使用禁止 | | list | push_back, push_front, erase(消したら次の要素を返す) | ++, --は定義されているが、+, -オペレータは定義されていない!やりたいなら、advance(it, n)とprev(it, n)を使うこと。 | | tuple | make_tuple, get | ほぼ何でもあり。unordered_mapに突っ込めない。 |
- メモの速度
- unordered_mapは定数倍が20くらいかかるので、できることならちゃんと配列でメモすること!
- かかる時間は、vector : unordered_map : map = 1 : 20 : 40 (5000要素)
- かかる時間は、vector : unordered_map : map = 1 : 20 : 60 (50000要素)
- スコープ外で一回定義してclearと、内部で何回も定義するのは、速度が同じ。
命名規則 †
- 添字の逆引きはinvをつける。
- 例えばvector<int> a;に対しては、unordered_map<int, int> ainv;
- int dx={0,0,1,-1}; dy={1,-1,0,0};は、使う添字の名前を借りてdi, djに。
イディオム †
- int a = -1;を異常値とすると、~a==1で正常値となる
- 2で割れるだけ割る: n/(n&-n)
- 一番下に立ってるbitだけを残して0にする: (n&-n)
- 最後に続いている0の数。NLZ(x) = count_bits( (x & (-x) )-1)
- 最初に続いている0の数。NTZ(x) = 32 - NLZ( (~x) & (x-1) )
- for all, there exists, goto文を使うとすごく簡潔でよい。
rep(s, 1 << n) {
rep(i, n) for (int j = i+1; j < n; j++)
if ((s & (1 << i)) && (s & (1 << j)) && !memo[P(i, j)])
goto no;
ret = max(ret, (ll)__builtin_popcount(s));
no:;
}
- 浮動小数点の比較は、<=ならゆるいから+EPS, <ならせまいから-EPSなどが明確にわかるようになる
( i < x ? a : b )++;
vector<int> v1, v2; ( i < x ? v1 : v2 ).push_back( i );
- repのメリット
- タイプ量が短い
- 変数名の変更に強い
- forは長いので、repなのか変な条件のループなのかわかりにくい
- 逆に for があったら注意して見る必要があるとわかる
|
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)