C

概要 †

  • 並列プログラミング技法のまとめ
  • TODO もっと簡潔に、勉強になる問題の抽出をしたい。
↑

参考 †

↑

メモ †

  • 手順
    1. 時間のかかっているところを特定
    2. プロファイラで時間計測
    3. 独立かチェック
  • バグ
    • デバッガを使うと再現しない可能性
    • 計算順序が違うので丸め誤差で計算結果が一致しない可能性
  • 並列コンピューティングのチューニング
    • 逐次の考え方
      1. キャッシュの非効率な共有
      2. 非効率なメモリアクセス
      3. バスのオーバーロード
    • 並列ならではの考え方
      1. 同期オブジェクトの競合
      2. スレッドごとの不均等な処理割り当て
      3. スレッドAPIの異常なオーバヘッド
      4. スレッドをそもそも使うまでもない処理量
  • 開発手順
    • 逐次のアルゴリズムを作ってから、並列化に移植すべき
    • アルゴリズムのバグか並列化のバグかがわからなくなるため
    • 即並列を組むのは慣れてからにしましょう
  • 各メモリに対して以下の4パターンを割り当てる。
    • 並行or排他
    • 参照or更新
  • スレッドの割り当て
    • 実行前に割り当てるのを静的
    • 実行中に割り当てるのを動的（各スレッドの実行時間が大きく違うorはじめにスレッド数が予想できない場合）
  • メモリ
    • 分散メモリ・共有メモリという概念がある（TODO）
    • TLS：スレッド固有なメモリが利用可能（とても重い！）
      • 変数のローカルコピーが必要で他の変数からも参照しないといけない場合
      • スレッドが同じ関数を別の場所からも呼ぶ必要ある場合
    • 参照＞＞更新の変数には、リードライトロックを利用するといい
  • タスク分解とデータ分解
    • 処理順序の独立性＝時間的独立性→タスク分解
    • データのそれぞれに対しての独立性＝空間的独立性→データ分解
    • OpenMPはデータ分解に特化したもの
  • タスク分解の原則（トレードオフになっていることに注意）
    1. スレッド数<=タスク数にする
    2. スレッドの処理量＝粒度＞オーバヘッド（つまり、なるべく粒度は大きい方がいい。スレッド数増加に対してもスケーラブルになりやすい。）
    • したがって、コアを全部使うと性能が下がることもある。
  • 依存性
    • 時間依存性
    • 空間依存性＝データ依存性（代入分だけ見ればわかりやすいが、ポインタがあると意味不明になる）
  • 独立性の増やし方
    • 漸化式を消す・帰納変数＝ループ変数をなくす・分割する
  • データ分解の要件
    1. データチャンク分割法
      • データの形状は、「隣接データ」と「交換＝外のチャンクのデータを使うこと」に影響
      • 経験的には、ボリューム-サーフェース比を最大にするのがいい
    2. チャンクを割り当てられたタスクが、更新すべきデータ全てにアクセス可能な保証
    3. スレッドに割り当てられたチャンクの状態
↑

Ben-Aliの並列化検証法 †

  • かなり重要。
  • 並列プログラムの理解
    • プログラムとはアトミックな処理の連続である
    • 並列プログラムはアトミックな処理をインターリーブする
    • 任意のインターリーブで期待した処理をする（この組み合わせは指数関数的に増える）
    • アトミックな実行文はいつかは実行される（公平性）
  • インターリーブ分析
    • 必要なこと：現状の定義、スレッドごとの処理の順番を考えること
    • 心配すること：デッドロック、スターベーション
  • クリティカルリージョン
    • 共有変数の参照変更
    • 必ず1スレッドからしか参照されないように、排他処理が必要
    • 他のスレッドがクリティカルリージョンに入っているときは、自分は入れない
    • いい加減にクリティカルリージョンを実装しようとするとだいたい問題が起きる（1-3段階）
  • デッドロックの4条件（これのうち一つでも不成立ならOK）
    1. 相互排除条件＝リソースを同時に取りうる状態が以下のどちらか「利用可能」「1スレッドのみが使用中のいずれか」
    2. 獲得後ウェイト＝リソース獲得済みのスレッドが、新たなリソースを獲得しようとする
    3. プリエンプトなし＝スレッドがリソースを獲得後は、そのリソースを削除できるのは獲得したスレッドが自発的にリソースを開放した時だけ
    4. 循環待ち＝スレッドの循環が発生し、和の中の次のスレッドがすでに獲得しているリソースを獲得しようとしている。
  • スターベーション
    • 条件はない。インターリーブ分析のみによって発見可能
↑

性能指標 †

  • 高速化比率
    • 1コア実行速度/nコア実行速度
  • コア数-高速化比率曲線
    • 理想的には係数1の直線になるはず。
    • そうならない場合はスケーラビリティが悪いという。
  • スーパーリニア
    • コア数を超える倍率の高速化
    • 原因はデータが小さくて、キャッシュにデータがすべて収まってしまうから。大規模データでテストしましょう。
  • Amdahlの法則
    • 逐次ソースコードを並列化することでどれくらいの高速化が可能かを予想できる
    • 並列処理可能割合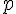$p$、直列限定処理割合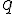$q$(p+q=1)、コア数nとして、処理時間はq+p/n以下にはならない。
    • これによって、コア数-高速化比率曲線が予想可能
  • Gustafan-Barsisの法則
    • 並列ソースコードがどれくらいの高速化を達成しているかを測定できる
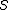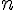    • 直列限定処理時間対全部処理時間$s$、コア数$n$として、高速化率はn-(n-1)s以下である。
  • 実行効率
    • nコア並列実行時間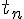$t_n$、1コア実行時間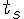$t_s$とした時、実行効率は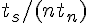$t_s / (n t_n)$
    • 低いとコアが使い切れていない
↑

具体的なライブラリ †

  • OpenMP, TBB, pthread, OpenCL(GPU)
  • OpenMP
    • ローカルコピーする変数の明示できる（private）
    • パラレルリージョンという概念があり重要（パラレルリージョンじゃないと使えない指示子があるので）
    • チャンクサイズはschedule指示節で指定
  • TBB
    • Lambdaが使える！
    • チャンクサイズを自動調節
  • pthread
    • より低次な処理
↑

具体的なアルゴリズム †

  • PRAMモデル
    • 配列を完全二分木とみなすことでアルゴリズムの高速化ができる
    • 並列和、プレフィックススキャンはPRAMに非常に向いている
  • プレフィックススキャン(例6.8)
    • 使い道：セレクション＝リスト（未ソート）からk番目に大きい数値を取り出す（O(n)で可能, 例6-12）
↑

MapReduce? †

  • Mapデータ構造をReduceするアルゴリズム
    • 分割統治法、バックトラック法など
  • 変形例
    • CountAndMark?では1つの合計→3種類の合計を一度に算出(6.3.3)
    • スキャン処理を用いてデータの値を解釈、論理バイナリのように処理
    • 配列を完全二分木とみなす (PRAM)
↑

ソート †

  • プロセッサ時間の80%以上はソートに費やされている
↑

性能解析ツール †

  • gdbはスレッドに対応
  • スレッドチェッカ
    • Intelスレッドチェッカはメモリ領域での衝突・デッドロックの可能性・スレッドのストールを検出可能
    • Intel VTuneパフォーマンスアナライザをのプラグインとして使うと、動的解析可能（ストレージコンフリクトを見つけるには、スレッドのメモリアクセスをすべて監視するなど）
  • プロファイリング（ホットスポットの特定）
    • gprofは-pgオプションでプロファイル用にコンパイルされたプログラムを解析可能。
    • Intel VTuneパフォーマンスアナライザ
↑

tbb †

↑

概要 †

  • マルチスレッド用の再帰可能なライブラリとコンテナ
  • tbbはメモリリークする（possibly lost, still reachable）
↑

機能 †

  • parallel_for, parallel_reduce, parallel_scan, parallel_invoke, parallel_pipelineなど
↑

チューニング †

  • tbbの粒度チューニング
    • 各処理ステップは1e4-1e5程度がよい
    • 自動粒度よりsimple_partitionaerの方がよい
  • grain sizeを10000程度にして、半分にしていく
  • blocked_range2dは1dより性能がよいことが知られているが、3dやそれ以上は複雑になるので実装されていない。自分で実装する異もできる
↑

並列化と代数構造 †

  • 参考
  • reduceとscanは半群で実現可能だが、モノイドや交換則も満たしてくれていると嬉しいこともある
  • 代数構造
    • 結合法則を満たす二項演算が定義され，演算が閉じている代数系を半群という（正整数，max, minなど）
    • 半群，かつ単位元を持つ代数系をモノイドという（非負整数）
    • モノイドかつ逆元があると群という（整数）（実は、半群から群を機械的に作ることが出来る）
  • 例
    • 与えられた環に係数を持つ n-次正方行列の全体は行列の加法または行列の乗法に関してモノイドを成す。
    • 有理数、実数、複素数、行列のどれもが積に関して. モノイドの公理を満たしている。
  • 計算機での具体例
    • tbb scanは結合のみ前提
    • tbb reduceは結合のみ前提
    • thrust reduceは結合＆交換前提
    • thrust inclusive_scan(exclusive_scan)は結合のみ前提
  • reduceは結合法則を満たす演算子のみで本来は良いが、交換もできると、積分画像や局所積分などがO(1)でできて嬉しい
↑

よくわからなかったところ †

1.3.2 1.4.2.2 2.1.1 キャッシュライン、キャッシュラインのデータの共有とは。 偽共有とは。実行効率の解析でよく出てくるので重要そう。 配列のパッキングとは
トップ   新規 一覧 単語検索 最終更新   ヘルプ   最終更新のRSS