プロコン
コーディングイディオム
非厳密アルゴリズム
概要 †
- アルゴリズムよく知らない人間の「一から自分で作ります!」ってメッチャ嫌な予感しません?
- 競プロすらできない人間が、一体何の役に立つんだ。
参考 †
目次 †
勉強すべきこと †
重要 †
- LPとして見るとポテンシャルは双対変数で、グラフアルゴリズムとして見ると負辺を消すために導入する量ですね(直感的にはポテンシャルの値は原点からの最短路長で、この時辺のコストは「最短路よりどれくらい無駄か」みたいなものを表します)
- 何故か最大流アルゴリズムで、負のコストがあるのにダイクストラを使って良い理由
- オフラインクエリに関するDecomposable searching problem
- lowlink
- 第2回ドワンゴからの挑戦状「花火」に対するシンプルな解法と最小費用流の双対 - とこはるのまとめ
- LCAの高速化
- オイラーとO(1)RMQが良かったって、かみぺーぱー先生が言っていた。
- Kahn's Algorithm (square君が天下一Aで出たと言っていた)
- Cartesian Tree
- monge
- ウェーブレット木
- 動的ウェーブレット木
- 永続ウェーブレット木
- 動的永続ウェーブレット木
- ウェーブレット行列
- Blackbox Algebra
- Link-Cut Tree(木で最強)
- インタバル木
- マージ可能ヒープ
- skew, 乱択、フィボナッチ、Pairingソートなど
- 分割統治法,逐次構成法,
- 平面走査法
- Gray Code
- 「パターンlの1文字目からマッチさせる場合は(自由度と引き換えに)スコアが増加する」DPの自由度とスコアの関係について
- cyclic shift
- Dominator tree
- dsu on tree
- 演算に結合性があるかの判定(決定論でO(N^2 log N) ランダムでO(N^2)でいける)
- Zobrist hash
- 最小包含円
- palindromic tree(eertree)
そこそこ †
- 最小全域有向木(m log n)
- topcoder 682
- りんごさんのd1eがランダムカラーリングで面白かったらしい
どうでもいい †
- ADS
- Treap, RBST(k-th tree), 平衡二分木
- デク・優先度付キュー
- ボロノイ図とデローネイ三角形分割
- 美術館問題
- Stern-Brocot木
- ベルヌーイ数列挙 O(n^2)
- 分割数 O(n√n)
- スターリング数 O(n^2)
- Chordal graph
- 点と直線の双対
- Stoer-Wagner
- 永持-茨木法 (全点対最小カット)
- Bairstow法
- スターンブロコット木
- 有向木の部分木のハッシュ
- Knuth-Morris-Pratt
- CIPR (最長共通部分列)
- 部分回文列挙
- Skip List
- Van Emde Boas tree (vEB tree)
- Fixed Universe Structures
- 永続的平衡2分探索木
- BK-tree
- Meldable heap
- 削除・更新のできる2分ヒープ
- Double-ended priority queue
- キュー with minimum
- Shunting-yard algorithm
- 平面グラフ 双対なものが構成できる。
- 木について
(1) 頂点uの値をxに変える
(2) 頂点u, vを結ぶ最短パスの頂点のうち、最小値を答える
というクエリを、O(log n)で処理できないという結論に至った。(今の僕には)
PolyominoEnumeration? †
ADS †
フロンティア †
- フロンティア法の長い解説
- BDD
- ROBDD
- Create Reduced Ordered Binary Decision Diagram (ROBDD)
- 変数に全順序関係が定義されている&限界まで簡約化されている
- BDDというとROBDDを指すことも。
- 構築は二つのルールを適用し続ければROBDDになる。冗長な接点を全て削除。等価な接点を全て共有。
- BDD 同士の演算 (Family Algebra) and, or, xor, not, ... みたいな色々な BDD 同士の演算ができる,便利
- 組合せ集合(集合族)を表現する ZDD(Zero-Suppressed BDD)
- 「計算爆発お姉さん」の問題が、O(nB)(n: fのビット数、B: BDDの頂点数)
- お姉さん本
- 集合族を表現するZDD
- BDDと違うのは、頂点削除のルールのみ
- BDDは「ここが0でも1でも結果が変わらない→頂点削除」
- ZDDは「ここが1だったらどうやっても結果が0になる→頂点削除」
- 疎な部分集合族を表現するのに適している
- BDD同様、ZDD 同士の演算がそのままできる(Family Algebra)
- フロンティア法
- ZDDはめちゃめちゃメモリ食う(1頂点当たりO(V))
- 実は、フロンティアの連結と次数だけ覚えれば十分
- その他
- 文字列集合を表現する SeqBDD (Sequence BDD)
- 置換の集合を表現する πDD (PiDD, Permutation DD)
計算複雑性理論 †
全探索 †
n^k †
- rep(i, ni) rep(j, nj) rep(h, nh) rep(k, nk) cout << i + j + h + k << endl;
深さ・幅優先探索 †
| 名前 | データ構造 | デメリット | メリット | | DFS | stack | 最適性は保証されない | 省メモリで全探索可能 | | BFS | queue | メモリをいっぱい使う | HITしたものが最短経路経路であることが保証される。BFSは回数小さい方固定の全探索 |
- 深さをメモするqueueの実装は、unordered_mapやmapが必要
- AOJ Reverse Sort
- そもそも深さ付きDFSはvectorをqueueとして使ったほうが楽
- queueでやりたいなら、queueに突っ込むnodeのunordered_mapを用意して、node tmp = q.top(); ll cost = depth[tmp]; q.pop();とかやるしかない。
グローバルにデータを持つDFS, BFS †
- 木の持つデータが大きい場合、「逆操作が軽い」DFSならば、メモリ使用量をO(1)に出来る。
- もし操作が「戻れる」なら、再帰関数を呼ぶ前と後に状態変化を書くことで、グローバルにデータを持てばよい
n! †
- next_permutation
- 局所する場合は挿入DPを使うのが良い
- 置換しても平均・分散・総和・二乗和などは保存する
- YES/NOしか求められていない時は、こういう情報の落とし方もある
nCr †
- next_combination
- めんどい場合はnext_permutationを使っても良い(Codeforces #395 Div1 C.)
総和を固定する全探索 †
- 数列aに対して、総和Sが含まれる評価式を満たすaを1つ挙げたい
- なぜ難しいか?
- aを動かすと、Sが動いてしまうこと
- 前から貪欲に決めていこうとしても、途中の更新で今まで確定していたと思っていた添字がだめになるケースがある。
- どうすればいいか?
- Sを固定すればいい!
- Sを固定した条件で、a[i]を構成していき、総和Sを実現できるかを見れば比較的簡単に全探索できる。
- SRM 697
- aの小さい方から確定させようとします。a[0:m-1]がすべてa[i]×(b[i]+1)>=Sを満たしていてa[m]が満たしていない時、a[m]をa[m]' = a[m]+kに更新するとa[m]'が条件を満たすとします。ここでa[0:m-1]の、もう確定したと思っていたものは確定したとは言い切れない気がします。なぜなら、以前に確定させたp<=m-1の添字に関する条件は、a[p]x(b[p]+1)>=S'=S+kとなり、元よりも条件が厳しくなるからです。
- しかし、S固定すると貪欲に取れて、最終的に構成されたa[i]<=Sならばa[n-1]をS-sum(a[0:n-2])とすれば合計がSのaが構成可能
総和がk以下の全探索 †
- 1=”1”, 2=”10”, 3=”100”, 4=”1000”... と 0/1 文字列に変換して考えてみる。
- 直前に現れた値が 1,2,3 だとすると”110100”と変換する。この文字列の長さは値の sum と等しい。つまり、前の値を合計が 16 以下まで保存するというのは、長さ 16 の0/1 文字列に対応する
10^18 †
約数全探索 †
探索範囲が2次元ある場合 †
- どちらかを固定するともう一方が厳密解が求まる可能性がある
基本 †
状態 †
- アルゴリズムでは「状態」が重要である。
- 全探索は状態を全て走査する
- DPは状態と遷移の組み合わせを考察する
- ゲーム理論ならgrundy数には状態が必須
- 全頂点にどんな情報を載せるか?というデータ構造みたいなものが決まると、自動的に処理が決まっていく
- どういう頂点に対して何を載せるか、という思考回路が足りてなさすぎるし、何が載っていると嬉しい、みたいな思考回路も足りない。CF 398 D2C
- 状態の抽象度
- 一見n!であっても、上手く見ると状態を減らせる、というのが非常に重要
- 順序 n!
- 一番一般的なもの。
- これをそのまま扱うためには挿入DPが必要
- 無理なら、貪欲法によって順序を固定するという選択肢がある
- 被覆+最後 n 2^n
- 被覆とは、集合のどれかを選ぶという意味。
- 巡回セールスマン問題
- 被覆 2^n
- 区間 n^k
- 1次元の区間は[l, r)で表される。
- 2次元の区間は[(a, b), (c, d))で表される
- 個数 n
- mod n
- 偶奇 2
- 関数形状をもつ
二分探索 †
- 使う場面
- 最小値・順位などを計算する場合、単調ならば二分探索を考えて常に簡単になる。
- 「 X の最小値を求めよ」と「X の最小値が m 以下かどうか判定せよ」という問題があったとき、前者が解ければ後者は解けるので、後者の方が常に簡単
二分探索のデバッグ †
while (1) {
ll t; cin >> t;
cout << check(t) << endl;
}
- 実装
- 二分探索の変数名をpassとfailとすると超わかりやすい
- l, rは厳しい
- パラレルバイナリサーチ=クエリまるごと二分探索
- Incrementalなデータ構造に対して、「〜であるのはいつか?」というクエリをQ個処理するのが基本形。
- O((Q q+t)log T)(qはクエリ応答計算量、tはデータ構造の構築時間)
- 永続の特殊バージョンの場合に使える二分探索
- クエリQ個を、IncrementalもしくはDecrementalな構築途中のデータ構造の時間に対して二分探索したいが、二分探索のための構築に時間がかかる時に使う
- より形式的には、Q個のクエリ先読み可能+クエリが時間に対して単調な場合、時間幅Tの永続データ構造に相当する機能を、省メモリでO((Q q+t)log T)で計算できるもの、と認識している
- Atcoder AGC 02D, yukicoder 416
- クエリ最小化
- Codeforces 499 D2Dでは、クエリを一回も無駄にできない制約で、f(x) (x in [2, 1e9])上の二分探索をする必要があった。
- ng = 1, ok = 1e9として、結果+1を聞くということをして、QLEを出した。
- 閉じてる区間の整数二分探索は、[2, 1e9]ならばng=1, ok=1e9+1と、一つずつ拡大しないといけない。
ダブリング †
- ダブリングは、f(x)=f(f(x-1))なる関数であれば、f(x)の計算がO(log n)で計算できる
- なぜなら、f(2^{k+1})=f(f(2^k))だから、f(2^k)を求めることが簡単。
- ダブリング上での二分探索は「〜を超えない最大の添字」を探す、と覚えると良い
- 例
- 木やFunctional Graphのある頂点から、n個上の親・n個上までの加算・n個上までのminを求める
計算量解析 †
- アルゴリズムイントロダクションでは、漸近的にタイトとは限らない上界O、漸近的にタイトとは限らない下界Ω, 漸近的にタイトでない上界o、漸近的にタイトでない下界をωと表している。なお、漸近的にタイトな限界をΘと表している
- 例えば漸近的にタイトとは限らない上界\( O(f(n)) \)は、ある\( n_c, c_0 \)について\( \forall n \ge n_c\ g(n) \le f(n) \)なる任意の\( g(n) \)の集合のこと
- 形式上集合であるが、これをなぜか\( g(n)=O(f(n)) \)と書くと都合が良いことがある
- 計算量は一般的には数学的帰納法によって解く
- マスター定理
- 計算量に関する漸化式を解くための3通りの公式。iwiwiさんの\( O(n^2) \)の木DPの計算量解析や、多倍長のリダクション\( O(n^2) \)などを証明できる。
しゃくとり法 †
- しゃくとり法
- 全ての左端に対してベストな右端を見つけるイメージのアルゴリズム
- 「各lに対してf([l,r))が単調増加二値関数の時、が真になる最小のrを計算」
- 区間から真偽を返すfが「f(S)が真ならf(広(S))は真かつ、f(S)が偽→f(狭(S))が偽かつ、f(空)=偽」を満たす時、真となる区間をこれ以上狭められないような区間を全列挙するアルゴリズム
- ある関数fは区間X=[l,r)→真偽値(例:ある区間和がS以上)
- fの単調性:f([l,r))が真→f([l-1,r])もf([l,r+1])も真。f(空)=偽
- f([l,r])が真かつf([l+1,r])もf([l,r-1])も偽となる、「もうこれ以上削れない区間」を全列挙する-例題
- 例題
- 非常に基本的な問題
- ARC 22B(39ページ目)
- ARC 30C
- 数学的解釈
- paiza
- 例題
- paiza
- 例題
- 例題
Monotonic Queue †
- 数列aが与えられる。全てのiについて、min a[i, i+w)を求めよ。
- これは、尺取り法でO(n)でできる
- 幅wに限定したが、尺取りの区間についてならば同様にO(n)
- (ちなみに、スライド中央値はw固定ならば、multisetを持ちながらやるとO(log n))
- 尺取り法
- 状態 = 「v = 区間[i, i+w)の最小値の位置mに対して、[m, i+w)の厳密な増加列の添字列」
- 遷移(左): a[i]よりa[v.back]が大きければ、ひたすらv.pop_backする。 v.push_back(i)。
- 遷移(右): v.frontがiならば削除
- 例
- a = [9 3 4 2 7 3 9], w=3
- i = 0; v = [1 2] (値は3 4)
- i = 1; v = [3] (値は2)
- i = 2; v = [3 4] (値は2 7)
- i = 3; v = [5] (値は3)
- i = 4; v = [5 6] (値は3 9)
- いわゆるスライド最小値はMonotonic Queueと一般的には言われている
- Monotonic queueは、再帰的に「q[i] = [q[i-1], r)の最小値」と簡潔に書くことができる。(a[q[i-1]]を認めるかは実装次第)
- Monotonic Queue qは数列で表され、
- q[0] = [l, r)の最小値
- q[1] = [q[0], r)の最小値
- q[2] = [q[1], r)の最小値…と繰り返される列のこと
- 計算上重要な性質は、
- [l, r)の最小値が常にq[0]であり
- かつl->l+1や、r->r+1にする操作がO(1)でできる、ということである。
- 具体的には、l->l+1の際には、q[0]がlならば削除するだけでよい。
- r->r+1の際には、qを最後から見てa[r]超のqを全削除してq.push(a[r])すればよい。
- お気持ち
- 「数列a[0, i)を見終わった後に、a[i]に何が来るかはよくわからないけど、解の候補となりうる位置の候補を全部列挙すると?」みたいなことを考えると、厳密単調性が保証される添字集合を考えたくなって、これは尺取れる
- 数列のquantile
- 範囲を尺取りみたいにしていいならO(log n)
- 上手くイテレータを操作すれば、普通のsetでもいい
stackテク †
- stackに不変構造を保存する。
- 最大長方形などstack系ははpopの時に更新するのがスマート(ARC 81F)
- popの時に更新する場合、最後popされていないものがstackに残ると悲しいので、最後に番兵を投げるのがよい。
問題の見方 †
- アルゴリズムの重要なことは、脳内の整理
- 図や表を多用しまくることが重要
基本的なこと †
- 凸凹してたら
- 全探索
- DP
- 半分全列挙
- 分枝限定法
- 枝刈り全探索
- マッチング
- フロー
- 二部グラフ(結局これもやってることはフロー)
- 割り当て(全体の拘束のもと、満足度を最大化)
- 「5歩で」「10回で」
- 半分全列挙
- AOJ Reverse sort, yukicoder 五輪ピック
- 「辞書順最小で」
- 辞書順は取れるときにとれば最適になる
- 待っていても良い物がこないし、一回一回で最適なものを選べばいいだけだから
- 「n<200のグラフ」
- Nが小さいグラフはとりあえずWFで全点から全点にすぐ行けると思うと良い
- 「全て異なる」
- 割り当て問題。「n人の人がm個の仕事をする。人iが仕事jをするときの達成度vのリストが与えられる。全体で最大の達成度はなにか。同じ仕事は複数人で受けられない。」
- 厳密に小さいと全て異なることになる。全部異なるものを仕事側とすると、割り当て問題の「同じ仕事は複数人で受けられない」に相当することになる。
- AOJ Dangerous Tower
問題の図示 †
##
###
#######
########
変数の動きの整理 †
int a; cin >> a;
b = a * a;
c = a * b + (a > 0);
a b c
--------
-1 1 -1
0 0 0
1 1 2
変数のまま網羅 †
- sに(1) a足す (2) bかけるを何回行えばtになるか??
- \( s+a \), \( sb \), \( sb+a \), \( sb^2+2ab+a \)などが作られる
- 一般化すると\( b^k s + a(c_0+c_1 b + ... + c_{k-1} b^{k-1}) \)で網羅できる!など。
発想 †
- 順像的に見る
- 逆像的に見る。
- 逆から塗りつぶしたら、塗り剥がしたらどうなる?(SRM 696 D1E Gperm, SRM 655D1E)
- 逆からループを回したら?(CF らてさんが神だったD2C問題)
テスト前のチェック †
- 回しきれていないループミスをひたすら探す
- 誤読
- assertしまくる
- 関数を分けて部分問題をassertしまくる
- コメント書きまくる。
用語 †
- multiset
- 同じ要素が複数入っていても良いデータ構造。eraseでは全部ではなく1個だけ消す(Codeforces 367 D2D)
- 部分列(subsequence)は、部分文字列(substring)とは異なることに注意する。前者は元の列の連続した項からなる必要はない。
データ構造の数学的構造 †
- いい感じのまとめ
- 代数的構造とアルゴリズム。特にsparse table とダイクストラ
俯瞰 †
- データ構造Gと演算○のセットを、(G, ○)という。
- これがどのような代数的構造を持っているかで、適用可能なアルゴリズムを限定できる。
- アルゴリズム構築に重要な代数的構造は以下である
| 名前 | 特徴 | 具体例 | | モノイド | 並列処理可能性 | (整数, min), (整数, max) | | 群 | 0-indexだけ計算すればi-indexに出来る | (整数, +) | | ベクトル空間 | 行列演算可能性 | (実数, +, *) | | 半環 | 行列累乗可能性 | (bool, XOR, AND) |
代数的構造のまとめ †
- 環からは、2つの演算子に関する代数的構造。
- 下に行くほど、制約が強い
| 名前 | 定義 | 具体例 | | マグマ | (S, ○)が全域性を持つ=演算結果も集合Sに入る。集合Sを台集合という | | | 半群 | ○が結合則を満たすマグマ(S, ○) | | | モノイド | 単位元eを持つ半群(S, ○) | (自然数, +), (自然数, *) | | 群 | 逆元を認めるモノイド(G, ○) | 二値転倒数のマージ則 (0の数, 1の数, 転倒数) | | アーベル群 | ○が可換な群(G, ○) | (整数, +), (有理数から0を除いた集合, *), (実数から0を除いた集合, *) | | 半環 | (R,•,+)、+下の可換モノイド、•下の半群, +上の•の分配性。逆元がなくてもOK | (自然数, *, +)。max-plus代数=(整数, +, max)は+が乗算なのが面白い! | | 環 | (R,•,+)、+下のアーベル群、•下の半群, +上の•の分配性 | Nは任意の自然数としてZ/NZ=(Z, * mod N, + mod N)は環、これは余剰環と呼ばれる。 | | 単位環 | •について単位元1を持つ環 | | | 可換環 | •の可換性を持つ環 | | | 整域 | •に対する非ゼロ因子付き単位元を持つ可換環 | | | 体 | 非ゼロ元の•に対する逆元を持つ可換環 | Z/pZ=(Z, * mod p, + mod p)は余剰体と呼ばれる。ただしpは素数に限る。またp=2の余剰体はブール体と呼ばれてZ/2Z=B=(Z, AND, XOR) |
- イデアル
- 環の特別な部分集合
- 「何を取ってきても、自分と乗算すると自分になっちゃう」(例: (整数, *, +)で、偶数はイデアル。どんな整数を取ってきても、偶数と掛け算すると偶数になっちゃう)
- 環は可換性を前提しないので、左イデアルと右イデアルがある。両側イデアルを単にイデアルと呼ぶ
- ベクトル空間について
- 体Fを複数連結した「体Fのベクトル」に関して加群であればベクトル空間になる。
- 「Vを体F上のベクトル空間とする」などと表現する
| 名前 | 定義 | 具体例 | | 環上の加群 | 左R-加群Mの定義を行う。アーベル群(R, +)と、RxM->Mを定義するスカラー乗法*について、+の分配則・スカラー乗法の結合則・*に対する単位源の存在を満たすならば、Mは左R-加群。 | | | ベクトル空間 | 体(G, *, +)に対して、+の分配則・スカラー乗法の結合則・*に対する単位源の存在を満たす | |
- annihilate
- 日本語では「零化」
- Rを環、Mを左R-加群、SをMの部分集合とする(大体R=実数, M=ベクトルの集合, S=ベクトル部分集合だと思えばいい)
- Rに関してAnn(S)={r in R | 左からrをかけるとSの全ての元が0になる}
- Ann(S)は左イデアルであるため、これを日本語では「零化イデアル」と呼ぶこともある。
モノイド †
| op | T | T0 | | max | int | 0 | | min | int | inf | | (+) | int | 0 | | (*) | int | 0 | | sort.(++) | [int] | [] | | ^(累乗) | int | 1 | | and | bool | 1 | | or | bool | 0 | | xor | bool | 0 | | (++) | string | "" | | 集合和 | [int] | [] | | 集合積 | [int] | 全体集合 | | gcd | int | 0 | | lcd | int | 1 |
- 非自明モノイド
- [l, r)の連続部分列の総和の最大、はモノイド(AOJ Do use segment tree)
- 結合法則と逆元が存在する
- 0-indexの計算だけで、i-indexの計算が可能という特徴がある。
データ構造の機能の名称 †
- 動的
- 木・配列・グラフなどの構造そのものが変わること。
- 動的凸包、動的kd-Tree、動的Ford Fulcarsonの場合、「削除ができること」という意味。
- オンライン
- 永続
- データ構造の途中結果に、更新が終わったあとにアクセスできること。
- 入門には永続Union-findが一番わかりやすい。
- だいたいのデータ構造は永続にできる。永続配列、永続平衡二分木(RBSTがよく使われる)、永続union-find、永続set、永続セグメントツリー、永続ウェーブレット木…
- 範囲更新
- [s, e)までに演算を行う、木の頂点sを根とする部分木全てに演算を行う、木の頂点sから木の頂点eの最短パスの全てに演算を行う、など。
永続 †
コンセプト †
- ノードに持たせるのが 1 つの値では不十分で,データ構造を持たせたいような際,親ノードとの差が小さいことを上手く利用して効率的に全ノードにデータ構造を持たせることができる
- 部分永続と完全永続
- 部分永続は最新版のみ変更可能だが、部分永続は全て変更可能
- 永続の種類
- 永続の制約
- 永続の反対はEphemeral
- 20分でわかるPurely Functional Data Structure?
永続配列 †
DFSでできる永続 †
- 逆操作が簡単な永続データ構造は、ただ「グローバルにデータを持つ」DFSを掛けばよいだけ。
永続BIT †
永続UnionFind? †
永続平衡二分探索木 †
- 融合永続まで行けるのは、AVL木。他にはマイナー過ぎるのを除けば赤黒木ですね
- RBSTは永続までは行けますがコピペみたいな融合永続になると死にます
bit manipulation †
| 名前 | プログラム | 特記事項 | | set_union | A | B | | | set_intersection | A & B | | | set_subtraction | A & ~B | | | negate | A ~ ((1 << size) - 1) | | | set(bit) | A |= 1 << bit | | | clear(bit) | A &= ~(1 << bit) | | | get(bit) | (A & 1 << bit) | | | count trailing zeros | __builtin_ctzll(bit) | | | count leading zeros | __builtin_clzll(bit) | | | count pop count | __builtin_popcountll(bit) | | | 空集合以外の全部分集合の列挙(mask) | for (ll i = mask; i > 0; i=(i-1)&mask) { cout << bitset<4>(i) << endl; } | 「空集合以外の」であることに注意。これを使ってDPする場合など。 | | 空集合以外の全部分集合の列挙(mask) | for (ll i = mask; i >= 0; i=(i-1)&mask) { cout << bitset<4>(i) << endl; if (!i) break; } | | | maskを部分集合に含むsize nのbitsetを全列挙(mask, n) | for(int i=mask; i<(1<<n); i=(i+1)|mask) { cout << bitset<4>(i) << endl; } | |
Union Find Tree †
- 連結成分の数え上げ
- Union Find Treeで、「頂点数-**異なる連結成分が連結された**回数」を計算すればよい
- これは全域木の辺の数を数えていることになる
有理数 †
整数論 †
modを取る意味 †
- 浮動小数点誤差によるバグと、アルゴリズムのバグを切り分けられる
- 10億7で割った余りからなる剰余体は体なので、ほとんど実数と等価な演算ができて、しかも厳密に答えが出る。
- したがって、実数を入出力とするアルゴリズムを新しく作るとして、提案アルゴリズムと、提案アルゴリズムに一致するはずの愚直アルゴリズムを、一旦10億7の余りで実装して比較する。これが一致すれば大体OKだろうということが分かる。
- また、10億7は結構自由度が大きいので、ランダム入力を2, 3個生成してその一致を見るだけで、実質ユニットテストの代わりになる。
- あと、なんかバグった時のリカバリが早い。浮動小数点系のバグって、1e6に1e-4を足してて大体似ているからOKっぽい…となりがちだが、剰余体だと変数に入っている値の大きさに大小を定義できないので、バグを特定しやすい。
巨大数 †
- 素数でmod取るのは何か(囲碁の局面数など)を数え上げたいときに複数mod並列で回して最後に中国剰余することがあるというのを聞いたことはあります
- 中国剰余定理はGNFSかなにかの実行時に巨大数を扱うためのテクとして使われているという話を聞いたことがある(32bit素数を多数とってmodで計算して復元)
分数のmod †
素数の密度は高い †
- y 付近の素数の密度は Θ(1/log y) なので、O(log y)個程度調べれば、一つは素数が見つかる計算
- 「これを用いると、n以下の最大の素数を計算せよ」を高速に求められる。
Z/pZ体の逆元 †
フェルマーの小定理による逆元 †
- *a^(p-2)が逆元となる。
- 重要なのは、pが素数でない場合には、逆元が存在するとは限らないこと!
- 逆元が存在しない場合は、ダブリングのようなもので代用することを考える。
拡張ユークリッドの互除法による逆元 †
- nのmod pでの逆元を計算する場合、nとpが互いに素であれば、\( (g, x, y) = extgcd(n, p) \)として\( g=gcd(n, p)=1=xn+py \)よりmod pを取って\( xn=1 \)となり、xが逆元となる。
- この方法では、pが素数でなくともn, pが互いに素であるだけでよい&ちょっと高速
- n, mが互いに素だけで生成された1/n mod mは一意? and どれくらい自由に演算して良い?
5の逆元(mod 13)を求める。
5y ≡ 1(mod 13)
⇔ ∃k 13k + 5y = 1となる整数yを求める
このk, yを求めるのはextgcdでできるので、yを持ってくればOK
ax mod b (a,b:定数、x:変数) †
- とりうる値はgcd(a,b)の倍数(超典型、AGC26B, CF499D2E)
N^M (mod p) †
- pは素数なのでフェルマーの小定理より、N^M=(N%p)^(M%(p−1)) (mod p)
- フェルマーの小定理
- a^(p-1) = 1 (mod p)
- より、あるkと0<=m<pについて、
- a^b = (a^(b/(p-1))) a^(b%(p-1)) (mod p) = a^(b%(p-1)) (mod p)
x^(2^n) †
- x^(2^n)はf(n)=f(n-1)^2,f(0)=xというふうにO(n)で求められます
nCr †
- n!と1/n!をO(n log mo)で前計算することで、nCrはO(1)で計算可能
nCm mod 素べき †
n! †
nCm mod 一般 †
sqrt(n) mod mo †
nCk mod mをm進数の桁ごとに †
ユークリッドの互除法 †
- \( b=qa+r \)について、\( gcd(a,b)=gcd(a,r) \)を示す。
- より一般的に、
- \( D_{a, b} \) = {a, bの共通約数}
- \( D_{a, r} \) = {a, rの共通約数}
- について、
- \( D_{a, b} = D_{a, r} \Leftrightarrow D_{a, b} \subset D_{a, r} \land D_{a, b} \supset D_{a, r} \)を示す。
- 証明
- 全ての\( d \in D_{a, b} \)について、db'=qda'+rなのでr=d(b'-qa')より、rはdの倍数。dは、aとrの共通約数であるため、\( d \in D_{a, r} \)である。全ての\( d \)について満たすので\( D_{a, b} \subset D_{a, r} \)
- 全ての\( d \in D_{a, r} \)について、\( b=d(qa'+r') \)なので\( b \)は\( d \)の倍数。\( d \)は、\( a \)と\( b \)の共通約数であるため、\( d \in D_{a, b} \)である。全ての\( d \)について満たすので\( D_{a, r} \subset D_{a, b} \)
- gcd(a, r)は必ず小さくなっていくので、a=0なりb=0となり、いつかアルゴリズムが停止する。
拡張ユークリッドの互除法 †
lint ext gcd(lint a,lint b,lint&x,lint&y){
if(b==0){
x=1;y=0;return a;
}
lint q=a/b;
lint g=ext gcd(b,a−q∗b,x,y);
lint z=x−q∗y;
x=y;y=z;
return g;
}
- 拡張ユークリッドの互除法は、
- 順向き計算と逆向き計算がある。順向き計算でgcd(a, b)を計算し、逆向き計算で\( g = a_i x_i + b_i y_i \)を満たす\( a_i, x_i, b_i, y_i \)を計算している。
- 順向き計算は、ただのユークリッドの互除法。
- 逆向き計算は、\( g = b x_1 + (a - [a/b] b) y_1 \)のうち、\( gcd(a, b), a, b, x_1, y_1 \)が既知である時、\( g = a x_0 + b y_0 \)の\( x_0, y_0 \)を求めよ、という問題を再帰的に解いている(答えは\( x_0=y_1, y_0=x_1-[a/b]y_1 \))。境界条件は\( g = g 1 + 0 0 \)。
ルジャンドルの定理 †
- \prod (0, k]で2で割れるものは何個か?
- \prod (p-k, p]で2で割れるものは何個か?
- 同じじゃないよ!p=17, k=3とか。累積和を使おう!
- \prod (2^n-k, 2^n]で2で割れるものは何個か?
除算回避 †
- modが素数pではない場合、除算回避のために再帰的な関数を定義する必要があることがある
平方剰余 †
- 奇素数pに対してmod pの場合、\( a \in [1, p) \)のうち\( a=x^2 (mod p) \)なる\( x \)が存在するような\( a \)の個数は、ぴったり\( (p-1)/2 \)個。存在しないような\( a \)の個数も、ぴったり\( (p-1)/2 \)個。
- 存在する場合、\( a \)を\( mod p \)での平方剰余であると言う
- 平方剰余判定
- 極めて簡単
- \( a \)が\( p \)における平方剰余である \( \Leftrightarrow \) \( a^{(p-1)/2} = 1 \)
- \( a \)が\( p \)における平方剰余でない \( \Leftrightarrow \) \( a^{(p-1)} = -1 \)
- \( p \)における平方剰余\( a \)のxを具体的に求める
- \( p=2 \)は全探索できるので割愛
- \( p=4k+3 \)なら簡単
- \( x=a^{(p-1)/4} \)である。\( x^2=a^{(p+1)/2} = a a^{(p-1)/2} \)だが、\( a \)が平方剰余であることは既知なので、平方剰余判定より\( x^2=a \)
- \( p=4k+1 \)の時はTonelli-Shank Algorithmを使う必要がある(めんどい)
中国余剰定理・Garner's Algorithm †
- x % m_i = a_iという形のアルゴリズムからxを復元するあるごりずむにはGarnerのアルゴリズムというのがある
- m_iが素数なら中国余剰
aのB進数の桁和はa mod b-1に一致 †
素数 †
- 素数系のライブラリは、隣接性を利用したものと、しないものを明確に分けなければならない。
- 隣接性利用: O(n log log n)
- 隣接性非利用: O(n sqrt(n))
- 素数の個数はO(n / log n)
- 約数の個数は、exp(log n / log log n) / 10個くらい。
- Prime系は特にint型やめたほうがいい気がする
- (こどふぉでミラールビンが使えないのあれなので、uint128を使わないのも用意したほうが良い)
構築付き素数判定 †
- エラトステネスのふるい
- 長い配列を用意して、必要のないところにはそもそも試し割りしないようにしながら素数を列挙する
- O(n log log n)
- Atkinの篩
連続する素数に関する問題は速く解ける †
- 具体的にはO(n sqrt(n)) -> O(n log log n)に落ちる。
- エラトステネスのふるいと同じようなアイディアで、試し割りするともに素因数の数を数えることで、隣接100万くらいの素因数なら全列挙できる。
- 具体的には、SRM 565 D1Mのように隣接100万個の素因数の数え上げはO(n log log n)と高速である一方、構築後の素因数を一つ一つ見るのでO(n sqrt(n))となりn=100万では無理。
非構築素数判定 †
- Millar-Rabin Test
- O(20)くらいで構築なし、64bitの素数判定ができる!
区間篩 †
約数全列挙 †
- sqrt(n)まで試し割りして、全部の割れたものに関して(i, n/i)を全列挙すればOK
ローのアルゴリズム †
- 極めて大きな素因数分解の簡単な実装(ruby, MRとローのアルゴリズムの組み合わせによる)
素数の数 †
- Meissel-Lehmer algorithm c++
素因数分解クエリを高速に行うための前処理 †
- osak法 http://www.osak.jp/diary/diary_201310.html#20131017
- 配列fac[W]を用意します(Wは最大値-1)
- エラトステネスの篩をやるとき、i*jを非素数と判定するときにfac[i*j]=iとすると、篩が終わったとき各整数xについてfac[x]がxの最小の素因数になっています(xが素数ならfac[x]==xとなるようにする)
- 配列facを持っていれば、整数vが与えられたときv/=fac[v]をv==1になるまで繰り返すことで、vの素因数の個数程度の手間で素因数分解ができます。
v=60
fac[v]=2
v/=2, v=30
fac[v]=2
v/=2, v=15
fac[v]=3
v/=3, v=5
- 「sum_{i in [1, 1e6]} iの素因数の個数」は3.6e6個なので、fac配列を持つことによる省メモリ効果は1e6で30%くらい?省メモリということは、計算時間もそれだけ短くなっているはずなので、素因数分解がO(1)からO(log n)になることで5倍程度の高速化がお手軽に得られるなら確かに強いか。
- 素数テーブル高速化のためにAtkin使ってるけど、エラトステネスでも素数テーブル構築できるようにしようかな。
区間 †
区間スケジューリング問題系 †
- 有名な貪欲:とりあえず右端ソート
- 「◯日から×日までの間に1日は働かなければならない」というルールさえ守ればいいなら誰でも期限ギリギリまで働くのを延ばし続ける
- 区間スケジューリング問題の双対
- 何か区間みたいなのがあって、「左端がx以下のもの」「左端がx以上のもの」「右端がx以下のもの」「右端がx以下のもの」「左端がxより小さいのもの」「左端がxより大きいのもの」「右端がxより大きいのもの」「右端がxより小さいのもの」みたいなのをlower_boundで見つけるみたいなのってどうすればよいの?左右・上下で4つset持っておかないといけないの??
- 少なくともused関数は不要だった(setがその役割を果たすので)
- 基本全比較関数で実装しとくしかないと思うけど、ラムダでやるのがこんがらがりまくって-x.firstみたいなのを突っ込んだ区間集合を別に管理した。これをやるととにかくinsert忘れたりerase忘れたりして慎重さにかける僕にはつらい
kd-tree †
- 区間の数え上げは2次元平面にプロットしてkd-treeになりがち
- 区間の唯一性は「直前が入っておらず直後が入っている」でカウントできる
範囲クエリ †
演算 †
| 演算 | 結合 | 可換 | 可逆 | | + | o | o | o | | * | o | o | o | | min | o | o | | | 行列積 | o | | | | 拡大回転行列積 | o | | o |
まとめ †
| 名称 | 結合 | 可換 | 可逆 | 構築後のデータ変更 | 構築 | 参照クエリ | 更新クエリ | 範囲更新 | 備考 | | Fenwick Tree = BIT | o | o | | o | O(n) | O(log n) 0-indexのみ | O(log n) | x | | | Fenwick Tree = BIT | o | o | o | o | O(n) | O(log n) i-indexも可能 | O(log n) | x | | | Sparse Table | o | o | | x | O(n) | O(log log n) | - | - | 出力の選択性を要求(演算はmin, 2番目のようなもののみ) | | Segment Tree | o | | | o | O(n) | O(log n) | O(log n) | x | | | Lazy Segment Tree | o | | | o | O(n) | O(log n) | O(log n) | o | | | いもす法 | o | | | x | O(n) | O(1) 0-indexのみ | O(1) | o | | | いもす法 | o | | o | x | O(n) | O(1) i-indexも可能 | O(1) | o | | | ナイーブ構築あり | o | | | o | O(n^2) | O(1) | - | - | | | ナイーブ構築なし | o | | | x | O(1) | O(n) | O(1) | x | |
BIT †
- Fenwickは、「点更新」「範囲参照(0-indexにしかならない!)」
- Fenwick Tree=BIT=Binary Indexed Tree
Segment Tree †
- Segment Treeは、「範囲更新」「範囲参照」(範囲更新はlazyによって実現)
- Segment TreeはBentley, J.L., “Algoritluna for Klee’s Rectangle Problems”, (1977)で初めて導入されたと言われているがかなり怪しいと思っている
- セグメント木
- モノイドでいいので応用力が高く、自分で考える部分が大きい。
- 「S([i, h]) = f(S[i, j], S[j+1, h])なるfが簡単な形で求まるか?」を考えると良い
- 平方分割でできるならセグ木でもできるだろう、と思考回路もありえる
- コツ
- 非遅延セグメントツリーは、結合二項演算と単位元だけあればできる。
- 練習問題
- range add gcd segment tree
セグ木に変なもの †
Lazy Segment Tree †
- 本当に遅延セグ木は要りますか?
- 取得が一点しかない場合、遅延セグ木を普通のセグ木で代替できる(yukicoder 悪くない忘年会にしような!)
- 遅延セグ木のコツ
- あるノードより上のノードとその子のlazyを、上から全部解消すると、そのノードの本当の値が出てくる。
- 「Segment [l, r)が値v遅延xを持っている時、range min(a, b)がSegment [l, r)を含むreductionを要求する場合、xが正しくないので遅延を解消しなければならない。だからその時にSegment [l, r)の遅延のみ解消するようにpushする」で解決したけど、結局僕の表現も厳密ではない。
- 自分を含めた祖先にlazyが0元ではないものが存在するならば正しくない
- 遅延セグ木の必要十分条件として適切な表現は「クエリ圧縮可能」
- 何かこれ、遅延セグ木の気持ちが書いてあって有用
- 遅延更新セグ木のアルゴリズム
- 更新すべき被覆X={X_i}を列挙する。以下i固定
- X_i以上に未解消のlazyがあれば、そのlazyを全て解消
- X_iの真下があれば、真下にlazyを追加
- X_iをdataに追加し、上方向に一貫するように更新
- 更新すべき被覆X={X_i}を列挙する。以下i固定
- X_i以上に未解消のlazyがあれば、そのlazyを全て解消
- 解消後のX_iをメモ
- op(X)を計算
- 実装
- コツ:1-indexで実装し、data[0], lazy[0]は使わない
- lazy segtreeに必要な条件、集合A上の+っていう演算結果が欲しくて、更新クエリが写像A -> Aの部分集合Fの元になっているとき、(A,+)がモノイドで、Fが合成で閉じていればokな気がした。あとはFの元f,gについて合成f*gとf(x_i)の区間和が高速に計算できれば
永続Segment Tree †
動的Segment Tree †
部分列の最大値を計算するSegment Tree †
- AOJ Do use segment tree解説資料参考
- Segment Treeの各ノードに必要そうな値を考える
- その区間の最大値ansは絶対必要
- その区間の合計allも必要そう
- 左端を含んだ最大値left、右端を含んだ最大値rightがあれば便利
- マージ則
- m.ans = max(l.ans, r.ans, l.right + r.left)
- m.all = l.all + r.all
- m.left = max(l.left, l.all + r.left)
- m.right = max(r.right, r.all +l.right)
Shift Segment Tree †
Segment Treeの応用 †
- D-queryのオンラインバージョンは永続セグ木で解ける…本当か???(多分本当ではない)
- D-query自体は、重複を除去するためになるべく右側に置いておく、という考え方で解ける
範囲クエリ上での二分探索 †
- つまり、範囲で見ると単調性が現れるものが、範囲クエリでの二分探索に相当する。
- 数列のminとmaxは範囲に対して単調になる。
- ''全要素が正ならば、積分すると単調になる
- segment tree上の二分探索が可能''
- Segment tree上の二分探索、要するに積分すると単調=全要素が正ってことなんだよね。
imos法 †
- コツ
- n要素配列の累積和なら、n+1個用意して0番目を単位元にする。
- 二次元でも累積和できる。
- imos法
- 意味論
- 累積和の逆法??なんだこれ
- 累積和の意味論
- 棒を横に並べた時、そのちょうどi個までを見た時の長さの総和
- また、sum[i]=i個の和、という意味になる
二次元Fenwick †
http://codingmelon.com/2015/12/17/range-sum-query-2d-mutable-leetcode-308/
二次元セグ木 †
http://algoogle.hadrori.jp/algorithm/2d-segment-tree.html
http://d.hatena.ne.jp/ishikado/20111130/1322657085
logicmachineさんの実装
https://github.com/logicmachine/LibCompetitive/blob/master/structure/segment_tree_2d.h
遅延二次元セグ木は?
クエリスキップ †
- 初期値が単位行列的だったり、ゼロ的な場合、クエリで変更されていない部分をスキップできる
- yukicoder 往復漸化式
ソート †
クイックソート †
バケツソート †
- バケツソート
- 静的配列にひたすら突っ込むだけのソート。O(n)でソート可能。1000万はいける。
- SRM D2E 671?
自分でソート †
- 優先度付きキューで自分でソートする
- SRM D1E スターウォーズのやつ
平方分割 †
- 平方分割は、深さ2の sqrt(N) 分木で、深さが2であることによって色々な操作ができるようになっている、という説明を見て、目から鱗が落ちた覚えがあるわ。
- バケット法=平方分割=sqruare root decomposition=sqrt(n)分木
- 範囲を扱う時に、平方に分割して記憶することで前処理O(n)、各クエリO(sqrt(n))を実現
- 応用力が高く、自分で考える部分が大きい。各バケットが2分探索木やBITを持ってたりする。
- 応用範囲は、バケット法>セグメント木。
- 速度はバケットO(sqrt(n))<セグメント木O(log n)
- 例題
クエリ平方分割 †
- Codeforces Educational contestのどこかのF
木平方分割 †
Permutation †
- 要するに個数が固定でほかはどうでもいいということ(もちろん長さに対して種類が有意に少ない場合にのみ有効)
並列二分探索 †
- n個の二分探索する必要がある場合に高速化される(きちんと表現して)
- 例題
- yukicoder 416
- AGC 02 D
- Stamp Rally
- LimitedMemorySeries1
- yukicoder 511
グラフ †
グラフに関する基本的名称 †
- 頂点
- 辺
- 入次数・出次数
- DAG
- 平面グラフ
- Functional Graph
- 頂点が入次数、出次数がともに1
- Topcoder Sunny Graph, Codeforces Educational 16くらいのやつ(Functional Graphはサイクル分解しなくてもダブリング出来るよ、という問題)
- 二部グラフ
- 二色彩色可能なグラフ
- 奇サイクルが存在しない!!!
- キャタピラグラフ
- ゲジゲジみたいになっているグラフ(パスに次数1の頂点が大量につながっている)
- 構築とかで考察を忘れる(ARC95F)
実装上問題 †
- グラフに容量とかいろいろつけてると平気で3倍くらい遅くなってTLEする
有名問題とそのクラス †
- 概観
- いろいろ長い問題名が出てくる。同じ名前で違う呼ばれ方がするので、以下に統一
- 問題=最小独立パス被覆問題、最小頂点被覆問題、最大独立集合問題、最小パス被覆問題、最小辺被覆、最大マッチング
- 性質=DAG、推移性、二部グラフ
- 最小独立パス被覆問題
- グラフの頂点を、非連結な何個のパスで全て覆い尽くすことが出来るか?
- 非連結なの部分が「独立」に相当している。重要。これがないと、多項式時間にするのに推移性が更に必要になる。
- DAGだと多項式時間で解ける
- 最小頂点被覆問題
- 頂点被覆=全ての辺が、選んだ点に接続するようにする頂点集合
- グラフの頂点に色を塗る。色を塗られていないところの隣に必ず色が塗られているようにしたい。色を塗る最小回数を求めよ(NP完全)
- |V|=最小点被覆+最大独立集合
- 一般にはNP完全
- 最大独立集合問題=最大安定集合問題
- 独立集合=辺で隣り合っていないような頂点集合
- 一般にはNP完全
- 最小パス被覆問題
- グラフの頂点を、何個のパスで全て覆い尽くすことが出来るか?二回同じ頂点を使っても良い。
- 推移性があるDAGだと、最小独立パス被覆問題に一致し、多項式時間で解ける。
- 最小辺被覆
- 全ての点が、選んだ辺に接続するようにする頂点集合
- 詳しくは
- 推移性
- 「a->bとb->cに辺があるならば、a->cにも辺がある」を満たすDAGに関する性質
- 推移性のあるDAGなら、最小独立集合問題と最小パス被覆問題と最小独立パス被覆問題は一致し、多項式時間で解ける [Dilworth 1950]
- 二部グラフ
- 二色彩色可能なグラフ
- 二部グラフでは、最大マッチングが多項式時間で求まる
- 二部グラフならば、最小頂点被覆=最大マッチング
- 奇サイクルがないのと同値!!!
複雑なグラフ構築のコツ †
- グラフ構築ゲーはname server作ったほうがいい(name server = 文字列からノードの番号を得るmap)
最短経路問題 †
- ベルマンフォードって何のために使うの?(LatteさんのSelf-constructing witchが1つの解答になるかも)
| 名前 | 計算量 | アルゴリズム | 特徴 | | ベルマンフォード法 | O(VE) | 前提:負の閉路がない連結グラフ。全辺を見て、現状より辺を通じたほうが良ければ更新。更新するものがなくなるまで行う | 負のコストを許容。負の閉路がなければOK。また、すべての負の閉路の検出も可能(更新が規定回数で止まらなかったら) | | ワーシャルフロイド | O(V^3) | | 全始点全終点。実装楽。 | | 実行可能ポテンシャルを使った全始点全終点 | O(mn+n^2logn) | | | | ダイクストラ法 | O(ElogV) | 前提:負のコストがない連結グラフ。コスト最小の未確定頂点を選び、そこから行ける頂点を更新して未確定頂点とする。これを未確定頂点がなくなるまで続ける。priority queueを使って実装する場合は「確定」の概念が明示的には入らず、コストが同じなら一番初めに処理した頂点が強いことで弾く | 負のコストを許容しない。 | | 経路復元 | O(E)かO(V) | O(V)は以前の道を記憶する。O(E)は以前の道をあとから探す | E: d[j]=d[k]+cost[k][j]なるkを探す。V: 更新時prev[j]を記録する。 |
- ダイクストラ
- 要するに集合拡大
- 拡大ルールは「集合から到達できる頂点のうち、最も小さいコストの頂点を拡大する」
- 実装にはフィボナッチヒープでBFSが高速
- 実装が2パターンある
- 先読みダイクストラではwhile(q.size())if(dist[q.top().se]>q.top().fi)はたかだかちょうどn回しか回らない
- 通常ダイクストラではwhile(q.size())if(dist[q.top().se]!=INF)はたかだかちょうどn回しか回らない
- 先読みは、「今までに見た最短」を記憶して枝刈りするので少し速い(がバグる)
- Atcoder ABC 51D(良問)
- 最短パスの部分パスも最短パス
- 頂点xを通る頂点s->頂点tの最短パスが存在→dist(s, t) = dist(s, x) + dist(x, t)
- 辺i=(a[i], b[i], c[i])を通る頂点s->頂点tの最短パスが存在→dist(s, t) = dist(s, a[i]) + c[i] + dist(b[i], t)
- 適当なことを言うと、最短距離問題は、最小性と唱えまくれば正当性が出てきます
整数重みの最短経路問題の方法 †
ダイクストラ †
- コストが1ではない時は工夫の無い普通のBFSで最小性は担保されない。いい加減に実装して有向グラフのBFSとして扱うと、頂点の個数だけ最悪頂点全ての再計算が必要になるのでO(V log E)ではなくO(V^2)になってしまう。
- 副作用を持つ遷移が有る場合、その遷移を合成する(今回の場合、(1)->(2)と、(2)と、(3)の遷移と考えた方が良い)
- ダイクストラのusedチェック後のdistは、絶対にwhile (!q.empty())のステップに対して単調増加する!なので、BFSと同じように見つかったら即返って良い!!!
- Radix heapを使うとダイクストラが速いらしい
動的ダイクストラ †
0n-BFS †
- ダイクストラと一致より速い。O(V)
- ダイクストラでは、priority_queueに同じ頂点が複数含まれる可能性がある!!!ので、遷移時に存在判定してはならない!!whileのループ内部でdistに代入する前での、到達性チェックが必須。
V={0, 1, 2}, E(from, to, cost)={(0, 2, 6), (0, 1, 4), (1, 2, 1) }, 初期にv=0, cost = 0とすると、
v=0, cost=0 q={(1, cost=4), (2, cost=6)} d[0] = 0
v=1, cost=4 q={(2, cost=5), (2, cost=6)} d[1] = 4
v=2, cost=5 q={(2, cost=6)} d[2] = 5
閉路検出 †
- 有向閉路検出→SCC
- 無向閉路検出→BFSで二度来たら閉路あり。
強連結成分 †
- 強連結成分
- Kosarajuのアルゴリズムはよく知られている。
グラフの縮約 †
- 有向グラフならばSCCによってDAGに、無向グラフならば二重辺連結成分分解(biconnected component, lowlinkとも言われる)によって木に潰すことができる。
- SCCで縮約すると、任意のグラフはDAGになり、トポロジカルソートができるようになる
- BCCで縮約すると、任意の無向グラフは木になり、木DPなどができるようになる
トポロジカルソート †
全域森 †
- 重要なのは「ループがない」こと
- 全域森のモチベーション (Minimum spanning tree, MST)
- なるべく少ないコストで全部繋ぎたい
- なるべく少ないコストでグラフのループを消したい
| プリム法 | O(ElogV) | 統合頂点群から未統合頂点への最小距離をメモする。未統合頂点のうち統合頂点群に最も近い頂点を探す。統合頂点群に追加する。頂点追加によって、最小距離が変わるので更新する。 | 最も近い頂点を貪欲的に追加する方法 | | クラスカル法 | O(ElogV) | 辺をコストの小さい順に並べる。コストの低い順に見て、閉路ができないならば連結していく。閉路ができることは連結先と連結元がUnion-Findで同一かによって検知可能 | 最もコストの小さい辺を貪欲的に選び続ける方法 |
Functional Graph †
- 全ての頂点が唯一の有向辺を持つようなグラフ。
- 木の頂点がサイクルでつながっている形をしている。
- 実は、サイクルを分解しないでダブリングできる(Educational codeforces 15のE問題)
最小パス被覆 †
- DAG上だと多項式時間で解ける
- 「DAGを無理やり二部グラフにしたもの」を「2V個の頂点V, V’を用意して、元のグラフx->yに辺があるならばx->y’に辺を張る、としたときの二部グラフ」と定義する
- DAG上での最小パス被覆(全頂点を通るような)は、|V| -無理やり二部グラフにしたものの最大マッチングである
最大流 †
- 完全ユニモジュラだったら整数計画問題を線形計画問題に落とせる
- 完全ユニモジュラ=任意の小行列の行列式が0,±1になる行列
- フローはこの整数計画に相当する。
- ランダムグラフでフローが何故か早くて、こういうのの計算量をちゃんと解析している
| やりたいこと | 名前 | 計算量 | | 一般重みつき最大マッチング | Edmondsの花分解アルゴリズム | O(V^3) | | 一般最大マッチング | | O(VE log V) | | 最大流 | Push Relabel | O(V^3) | | 最大流 | Ford Fulkerson | O(FE), Fは流量 | | 最大流 | Dinic | O(E V^2), 辺容量全部 1 の Dinic は O(Esqrt(E)) | | 最小費用流 | Primal Dual | O(V^2 U C) | | 最小費用流 | Primal Dual | O(F E logV), ベルマンフォードを使っているので負コストにも対応 | | 二部グラフ最大マッチング | Hopcroft–Karp | O(E V^0.5) | | 二部グラフ最大マッチング | 最大流なら何でも | | | 二部グラフ重み付き最大マッチング | 最小費用流なら何でも | |
- マッチングの貪欲
- ある順番で辺を見るとして、(1) 辺eを見る (2) マッチングできるなら貪欲にマッチング (3) 辺を消す、を繰り返す時に(1)で辺の端点のいずれかの頂点の次数が1なら、貪欲にそのへんをマッチングさせても良い。
- 別に木に限った話ではなくて、一部にループがあっても、適宜次数1の頂点を含む辺はは消していってOK。辺e=(次数=1, 次数>1)を使わない場合、次数>1の頂点は必ずマッチングに使うべきである(なお、区別出来ない頂点は縮約可能)。
- 木の最大マッチングはO(n)。
- 最大流は頂点に情報が乗り、最小費用流は辺に情報が載ってるように見える…
- 双対
- AOJ How to Create a Good Game 解説1 解説2
- AOJ Longest Shortest Path 解説
- ‘’「最小費用流において、辺は制約条件1つを表現する!」’’
最小費用流 †
- 最小費用流は割り当て問題を解ける。
- 「全体で限られた資源で、個々人が資源を使うことにより個々人の不満度が定義され、その不満の総和を最小化する」ということができる
- 「全体で限られた資源で、個々人が資源を使うことにより個々人の満足度が得られ、その価値の総和を最小化する」ということができる
- 最小費用流の非常に良いテキスト
- 輸送問題
- 割り当て問題
- 複数シンク
- 特定の枝に少なくともこれだけのフローを流す、といった制約も解説
- 特にオアシスの例は非常にわかりやすい
- 輸送問題
- AOJ Dangerous Tower
- Dangerous Towerでなんでダミー変数が必要なのかわからん…
- マッチング問題
- n, mの数の点群p_i, q_jがある時、マッチングをk個作りたい。その距離の総和をなるべく少なくするためにはどういうマッチングをすればよいか?
- 二部グラフの最小費用流
- 二部グラフだと、ハンガリー法が定数倍の意味で高速O(n^3)。nが10000くらいならこれでOK
- メモリが足りない場合は、枝刈りしておいてO(V E log V)とかにするとよい
- ほんま雑でいいばあい、距離小さい辺から貪欲にとって、取ったらその辺のsrc, dstをもう使ったというふうにメモをする。これだけでO(E log E)の最適解の50%を保証する解答を得ることができる。ちなみに、LAMというO(E)の解法もある(実装めんどい)
- n, mの数の点群p_i, q_jがある時、マッチングをなるべくたくさん作りたい。距離の最大値をなるべく少なくしたい。どういうマッチングにすればよいか?
- 距離d以下を枝刈りしておいた二部グラフに対して、最大流をford-furkersonする。定数倍高速。
二部グラフ †
- グラフから二部グラフ構築はたったのO(n)
- 二色彩色可能ならば、塗った白黒を左右に振り分けて、必ず二部グラフを構築可能
- 二食彩色不可能ならば、二部グラフは構築できない
- AOJ RabbitWalking?
マッチング †
- 一般グラフの最大マッチング
- Gallai-Edmonds分解
- 二部グラフで重みが1ならfordfulkerson
- 二部グラフで重みが1とは限らないならば最小費用流かhungarian法
- 1人の人が複数の仕事をしてもいいばあいはsrc->人の頂点の容量を2とかにしておく
ランダムカラーリング †
最短経路として使われる辺 †
- クエリv, u, e = 「vからuへの最短経路として、辺eを使うものがあるか?」はd(v,e.fi)+cost(e)+d(e.se, u) == d(v, u)でO(1)判定可能
- 幾何的に見たら最短経路で要らない辺⇔3つなり4つなり見て辺の長さで多角形を作った時に多角形が作れない長い辺
最大クリーク †
- MCS
- マックスクリークサーチが爆速
- 富田悦次って人の書いた論文
補グラフ †
- 補グラフを取ると二部グラフになるような問題が多い
- POJ 3692 Kindergarten は、「補グラフをとると二部グラフになるようなグラフ」の最大クリークを求めなさい
- Independence [AtCoder? Regular Contest 099 E]
最大流 †
- マッチング問題が解ける(AOJ Luigi's Tarvan)
- Ford Fulcarsonを動的にする問題が大量にある
- 残余グラフ
- Ford Fulkersonでは、「流せる余力」を表したグラフを作る
- 元のグラフと何が違うかというと、「さっき順方向に2だけ流したから、逆方向に2だけ流す余力がある」というのを許可する点。
- これを前提すると、大概の操作が貪欲に行うことが出来る!
- また、流れているフローを、順方向の辺に対応する逆辺の容量を見ればよい。
- 動的Ford Fulcarson
- 辺Add:
- 残余グラフの余力が増える→フローが流せるか試すだけ。簡単
- 辺Erase:
- フローが流れていないなら、消すだけ。flowは変わらない。
- フローが流れていれば、まずその辺のフローを他のルートに押し付ける!これは、辺を含む閉路が存在したら押し付けることが出来る。
- その結果フローが流れなくなったら、消すだけ。flowは変わらない
- もしフローが足りないなら、終点から始点への消すフローFの増加路を押し戻す。そうすると、上記閉路が必ず存在するようになるので、他のルートに押し付けて、自分は消える。
最小カット †
- 幾つかの要素に 2 つの状態を割り振り,何かを最大化/最小化する問題で,更に DP ではとても解けそうにない場合,最小カットを疑うとよいです。
雑多 †
- 葉を指定した最小全域木→Kruskalの変形
- 分散最小全域木、比最小全域木などは、パラメータ化して何かを止めると凸にする
- k-th最小全域木
最大独立集合 †
一筆書き †
- オイラーの公式
- 一筆書きの定理
- これって平面グラフじゃないと成り立たないの??
- 実は、拡張版があって、連結成分数が入ったものもある。
- オイラーの公式 G の頂点数が n,辺数が m,面数が f ,連結成分数が k のとき, n − m + f = 1 + k
埋める燃やす †
- sからtへの有向グラフを以下のように構成する
- sが常に赤、tが常に青とした時、グラフを赤青に塗り分ける方法のうち、最小コストのものを計算することができる。
- コストの定義は、「辺のsrcが赤かつdstが青ならば、コストc」
- ここでは、グラフの構成法の意味論を書く
- 意味論
- ノードxには、「赤に塗る状態」「青に塗る状態」を割り当てる(定義通り)
- x->yがある場合、「xが赤かつyが青の時のコスト」を表す(定義通り)
- s->x->tとした時、s->xは「xを青に塗るためのコスト」、x->tは「xを赤に塗るためのコスト」
- 「xが赤ならば、yもzも赤」は、x->yとx->zにinf
- 「xが赤ならば、yもzも赤」は、x<-yとx<-zにinf
- 「xが赤かつyが赤ならば、報酬r」は、まず新しい頂点wを作る。s->wにr、w->tに0, w->xにinf, w->yにinf
- 「xが青かつyが青ならば、報酬r」は、まず新しい頂点wを作る。s->wにr、w->tに0, w<-xにinf, w<-yにinf
- 重要な制限(負辺ができるので)
- xが赤かつyが青で、報酬rは不可能
- xが赤かつyが赤で、コストcは不可能
- 注意
- ノードごとに赤青の定義を入れ替えることができる。
- 意味論を見ればわかるように、赤と赤の連動みたいなものを表現するためには、色の定義をうまく割り当てないとグラフが作れない可能性がある。
最近点対 †
平面グラフ †
- Lindström-Gessel-Viennot lemma
静的木 †
- 木の構造そのものが切られたり追加したりしないものでの、様々な木の上でのクエリの処理方法
- 木いろいろ
基本的な性質 †
- 頂点n辺n-1かつ連結なら必ず木構造
- 木構造はどこを根にしても木構造
まとめ †
| 名称 | 計算量 | 説明 | | 頂点から根へ向かうパスの二分探索 | O(log n) | ダブリングで可能 |
| 名称 | 結合 | 可換 | 可逆 | 構築後のデータ変更 | 木の構造変更 | 構築 | 参照クエリ | 更新クエリ | 備考 | | オイラーツアー+Segment Tree | o | o | | o | x | O(n) | O(log n) | O(log n) | min, maxもできる |
| 名称 | 結合 | 可換 | 可逆 | 構築後のデータ変更 | 木の構造変更 | 構築 | 参照クエリ | 更新クエリ | 備考 | | オイラーツアー+Segment Tree | o | | o | o | x | O(n) | O(log n) | O(log n) | min, maxはできない | | Heavy-Light Decomposition+Segment Tree | o | | | o | x | O(n) | O(log^2 n) | O(log n) | min, maxもできる | | Heavy-Light Decomposition+Unbalanced Segment Tree | o | | | o | x | O(n) | O(log n) | O(log n) | min, maxもできる。行列もできる。遅延・永続もできる。 [[yosupoさんのブログ参照http://yosupo.hatenablog.com/entry/2015/10/02/233244>]] | | Link-cut Tree | o | | | o | o | O(n) | O(log n), 最悪O(n) | O(log n), 最悪O(n) | min, maxもできる。行列もできる。 遅延はできるが、永続はできない。yosupoさんのブログ参照 |
オイラーツアー †
- オイラーツアーはDFS順序とも呼ばれる。
- 2種類あるので注意!
- bfsの経路を添え時に直したもの
- 木を列で扱える!
- しかも、各頂点番号が最初に登場するインデックスと最後に登場するインデックスの間が部分木に。
- 上から下への辺の重みも、上から下への経路で無向グラフ辺を足したものとして表現できる。
- セグメント木などのデータ構造を扱えるようになる!
- 部分木のコストを変える・部分木のコストのsum, min, maxを求める。(無向辺のコストを両方向正にして実現)
- 辺(上から下へに限定)のコストを変える・u から v へのパスのコストのsum, min, maxを求める(無向辺のコストを片方1片方-1にして実現)
1 2 3 2 3 2 1 2 3 2 1 // オイラーツアー
1 [2 3 2 3 2] 1 2 [3] 2 1 // 頂点に対応する部分木
1 [2 3 2 3 2 1 2 3] 2 1 // 最小要素の判定区間→1が最小で、この区間で1を持つ頂点がLCA
直属の親子のパスの頂点に乗ったデータの積分 †
- 頂点に群のデータを載せるタイプのオイラーツアーで実現できる。
- 木Gが与えられる。
- 木Gの根からの、オイラーツアーEを考える。
- |E| = 2*|G|
- 頂点iがオイラーツアー上で出てくる1回目を、f_i, 2回目をs_iとする。(fはfirst, sはsecond)
例)
0
1 2
3 4 5
のオイラーツアーは
0 1 3 3 1 2 4 4 5 5 2 0
f = [0, 1, 5, 2, 6, 8]
s = [11, 4, 10, 3, 7, 9]
である。
- 前提
- 木Gの頂点には、結合二項演算opと合わせて群をなす型のデータAを持っている。
- 頂点x, yについて、xがyの直接子孫とする
- [x, y]を頂点xから頂点yへの最短パスの経路上にある頂点(端を含む)とする
- やりたいこと: [x, y]のデータ型の積分をしたい。
- 具体的には、例でx=0, y=6とすると、#0 op #4 op #6を高速に計算したい。
- 実は、これはデータ型の群的性質を用いると、簡単に計算できる。
- データの保持をオイラーツアーと同じ長さの配列Dで持つ。
- 頂点iのデータをA_iとすると、を、D[f_i] = A_i, D[s_i] = A_i^{-1}と、初めの出現に普通に格納し、二回目の出現には逆元を格納する。
- ここで、[x, y]でのデータのopによるパスの積分を考えると、これは数列上で、D[s_x:s_y]の積分に一致する!
- 今データ型は逆元を持つことを前提としたので、D[s_x:s_y] = D[0, s_y] - D[0, s_x-1]であり、BITによってO(log n)で計算可能である。
- 今までの議論では、「xはyの直接祖先」を前提していたが、LCA(x, y)を求めることができれば、最短パスの積分もO(log n)で計算できる。
- The Euler Tour representation of trees was originally used in fast parallel graph algorithms (R.E~ Tarjan and U. Vishkin, An efficient parallel bieormectivity algorithm, SIAM J. Compur 14 (1985) 862-874. ).
頂点から根までの列の二分探索 †
重軽分解 †
- 用語定義
- Centroid Path Decomposition
- Heavy-Light Decomposition
- 親の子数が、「最大子数をもつ子」の子数の倍より以下ならばHeavy(つまり、1つのノードからHeavyな辺が二つ以上は出ない)
- 本当は、Centroid Path DecompositionはHeavy-Light Decompositionの一種、という言い方が正しい。
- プロコンではCentroid Path Decompositionのことを、Heavy-Light Decompositionと言及することが多い
- pekempeyさんのHL分解を使って木の上のクエリに高速に答える方法を紹介してくれている
トポソされた木の制約 †
- For each i, parent[i] will be between 0 and i, inclusive.
- 有名な木の制限
- 任意のグラフに対して、この条件だけで、
- 木だし
- ループないし
- 自己ループないし
- 多重辺ないし
- 予めトポソされている
- トポソされている木は、以下で超簡単に深さが求まる(配る再帰が、再帰不要になる!!(集める再帰は??逆から見ればOK?))
rep(i, n) if (i) {
d[i] = d[parent[i-1]] + 1;
}
heap †
- decrease_key
- dijkstra法で使用すると計算量が落ちる
- 実用速度としてはシンプルな二分ヒープ+読み捨てに勝てないが
- 整数なら基数ヒープはかなり早いが
再帰 †
返り値をメモするタイプの再帰 †
int f(int i, int j) {
if (i < 0 || j < 0 || i >= n || j >= n) return 0; // 入力異常条件
if (memo.count(P(i, j))) return memo[P(i, j)]; // もう答え知ってる
int ret = 0;
rep(d, 4) ret+=f(i+di[d], j+dj[d]);
memo[P(i, j)] = ret;
return ret;
}
条件を満たし続ける再帰 †
- 異常条件→メモ条件→メモ→自分→遷移→return
- 処理されているということは、必ず条件が満たされている、という再帰
int f(int i, int j) {
if (i < 0 || j < 0 || i >= n || j >= n) return 0; // 入力異常条件
if (field[i][j] != 'o') return 0; // 探し物じゃない
if (memo.count(P(i, j))) return 0; // もう来てた
memo[P(i, j)] = true; // 次からは来ない
int ret = 0;
ret += point[i][j]; // 自分を取って
rep(d, 4) ret+=f(i+di[d], j+dj[d]); // 近くのを取りに行く
return ret;
}
座標圧縮 †
絶対値 †
DP †
- 関数\( f(s) \rightarrow t, s \in S \)を考えて、それぞれの状態\( s \)について遷移後状態\( T_s \)を考える。\( s = g(f(t_1), f(t_2), \cdots, f(t_{|T_s|})) \)を計算する方法。ただし、T_sにエッジを張ったグラフがDAGである!
- DP の遷移とか書きながら詰める訓練を積んだほうがいい。「いける」って思ったら細部詰めずに書き始めよう。
DPの状態 †
- DPの状態集
- 「i人見て」
- 「直前maskで」
- 「j人余って」
- 「i人、i人グループ以上を許容するという制約を付けて」
- 「直前にAが出てきたのが添字iで」
- 「S の残りの部分に対する処理を行う方法」の個数のように、前を状態に持つのと後を状態にもつのと両方あり得る。こういう後が不明なDPの場合、「i番目を観測して、どういう状態がありえたか?」を網羅して足し合わせる感じ
- 「DPで状態をNにしたいならばどこかに境界線を引かざるを得ない」という直感。境界で状態を持つ MUJIN 2018 F
DPの見通し †
- 配るDPは大きめに作っておいて、必ず全状態を操作する。
- もらうDPは大きめに作る意味が無い。
DPに関する愚痴 †
- DPはとにかく、ある状態にいる人の気持ちになって考える=状態を固定した時に、次にどこに行くか、を考えることが非常に大事
- 難しさ
- 分かったつもりで実際に問題をといても、アクセプトされない。
- デバッグしにくいので、しかも何でアクセプトされないかわからない。
- 解説を見ても、DPは図を書かないと絶対理解不能。漸化式を文章で書かれても困る。
- DPの類型化
- 本当はやりたい。
- 無理矢理でもとにかく大量の(200問以上の単位で)ものを分類したい
参考 †
DPの漸化式 †
- コツ
- 「i未満の添字を使って」という表現をする
- 「〜が確定している時」という表現をする
DPの種類 †
| 名前 | 特徴 | できること | | 戻るDP | 漸化式の方向が逆のもの | 特になし | | 配るDP | 漸化式の関数が可換、かつ漸化式の関数に単位元が存在し、かつ更新前の添字から更新後の添字を計算可能 | 実装が楽。配れないならcontinueできる | | 集めるDP | 更新後の添字から更新前の添字を計算可能 | 汎用的 | | 前回のみに依存するDP | 空間計算量が抑えられる。DP配列を2だけ用意して偶数奇数で分ければいい。配る前回のみに依存するDPは初期化に注意 | | | 使い回すDP | 前回のみに依存し、かつ更新式が後ろにのみ依存する場合、添字を前から後ろに回して、空間計算量を更に抑えられる。DP配列を使いまわせるので。 | |
| 制限するDP | 考える添字を、条件によってうまく使い分ける。Codeforces 416 D2C |
DPのデバッグ †
- コツ
- 変更後の状態を
- 別のループで
- 自明でないものだけ出力!
DPはメモ化再帰のループ版 †
- メモ化からの漸化式構築=動的計画法
- 「これまでに得られる〜」をメモ化する
- 幅・深さ優先探索のメモ化のときに保存した状態と、ここで計算するテーブルの状態変数は一致する
- 「ありえない組み合わせ」というものが存在する
- DPは指数計算量探索の合流である
- 探索の「状態」と「合流法則」を抽出したものがDPとなる
- まず指数計算量探索を図示してみる
- 丸の中に状態(=添字や重さや価値)を書いたグラフを書いてみる
- すると、合流を見つけることができる。合流のルール(=その上流すべての情報の集め方)を抽出する
- 状態と合流から自動的にDPが計算できる
- 初期条件は初めが決まっていることも、深いところの拘束条件があることもある
- DPでは深いところしか決まっていないとやりづらい
- 場合の数も、初めに自明に決まる場合の数から始めるとDPが楽になる
何を考えるべきか †
- 自明な条件(=初期条件)はないか
- 「1個も取らないと答えは自明に0」
- 「最後の1つだけを取ると自明に1」
- 1セット
- 状態を適当に定めてみる
- 今の状態から次の状態がどう決まるかを考えてみる
- 次の状態が今の状態から統合されるかを考える
- 何の情報が足りないかを考え、情報を状態に追加する
全探索との対応 †
| グラフ分析 | メモ化探索 | DP | | 状態 | ノード | 引数 | DPテーブル添字 | | 値 | ノードに付属する値 | 返り値 | DPテーブル | | 遷移 | 上から下への操作 | 再帰関数(更新) | 漸化式(代入演算) | | 結合法則 | 二つ以上のノードから一つへのリダクション | 再帰関数(結合) | 漸化式(左辺値) | | 初期条件 | 初めのノード | 関数呼び出し | 境界条件 |
使い回すDP †
- テーブルを使い回して空間計算量と、計算時間の定数倍高速化ができるDP
- 考察を頑張ると実装が楽にタイプのテクだから乱用していきたい
- 定数倍時間早くなる理由
- テーブルに値がデフォルトで入っているので
- 自分に何もしない遷移がある場合に、速い。配るDPでchmin(dp[i+1][j], dp[i][j])があるケースなど。
- 配る場合、デフォルトでdp[i+1][now] += dp[i][now]がなされる(これが嫌ならばdp[i+1][now]-=dp[i][now]をしておく)
- 集める場合はデフォルトでdp[i+1][j] = dp[i][j]がデフォルトで入っているが、これは始めてそこに遷移できる場所なので、嫌ならばdp[i+1][j] = 0としてもよい。
- 使える問題クラス
- 集めるDPでは一般的にはdp[i+1][j] = f(dp[i+1][0, j), dp[i][j, n))のみに依存する場合に使い回すDPができる
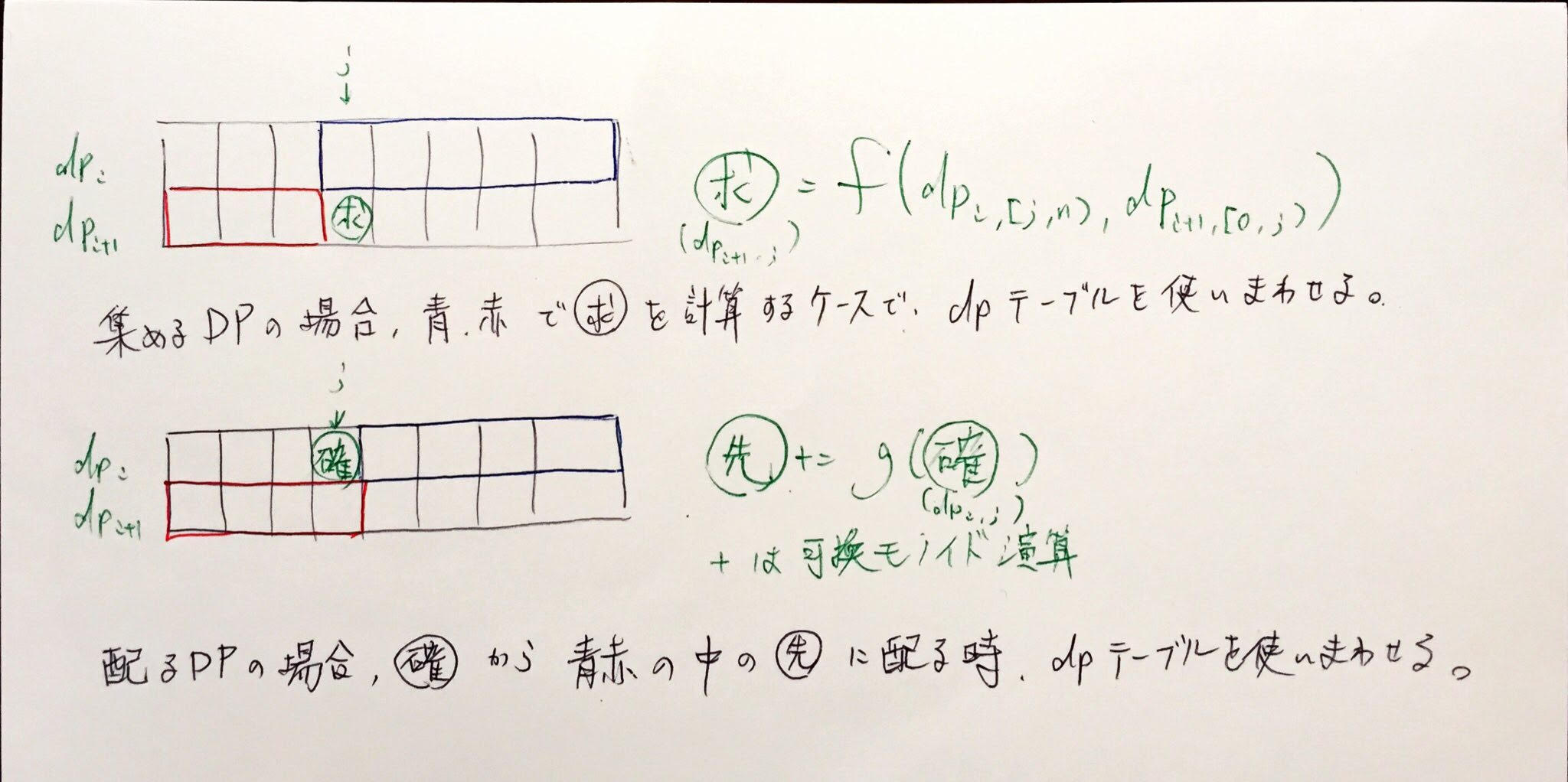
- 配るDPではこれにfが可換モノイド演算のsumの形式になっている必要がある
- 配る・集める向きが逆でも、逆向きに見る使い回すDPで行ける
桁DP †
- A未満の非負整数を数えるが入門に非常によいと思う。
- A: N桁の数字
- dp[i][j]: 以下の状態の時の場合の数
- i: 上からi桁目の自然数集合において (i=0, 1, ..., N, inclusive. つまりi=0では空集合を見ている)
- j: A未満であることが確定している (j = 0, 1)
#include <iostream>
#include <string>
#define rep(i, a) for (int i = 0; i < (a); i++)
using namespace std;
CTRL: Left Allegro Hand controller initialized.
const int mod = 1e9 + 7;
int dp[101010][2]; // pos, less
int main() {
string A;
cin >> A;
int n = A.length();
dp[0][0] = 1;
rep (i, n) rep (j, 2) { // DPテーブルの結合則の数 「DPテーブルから決まっていく様子を想像する」というのはこれを思い浮かべること。
int lim = j ? 9 : A[i] - '0';
rep (d, lim + 1) { // DPテーブルの結合則の具体的な計算数。「DPテーブルから決まっていく様子を想像する」というのはこれを思い浮かべること。
(dp[i + 1][j || d < lim] += dp[i][j]) %= mod;
}
// dp[i + 1][0] = dp[i][0]; d[i + 1][1] = (A[i] - '0') * dp[i][0] + 10 * dp[i][1];
// でもいいはず。でも与えられたdによってDPテーブル添字が一意に決まるので、上のようにdで全探索している
}
int ans = 0;
rep (j, 2) (ans += dp[n][j]) %= mod;
cout << ans << endl;
return 0;
}
- たまに、「上からi桁見て後が全部0で埋まっている…」みたいなDPが必要になることがある。(ARC52 D)
実装の構造 †
dp[初期状態] = 初期値;
for (状態) {
for (遷移) {
次の状態 = 遷移(状態);
dp[次の状態] = dp[状態];
}
}
// ↓のようにコメントを書いておくとよい
dp[i + 1][k][j] = (dp[i][k][j] //i番目は選ばない
+ dp[i][k - 1][(j - i + N) % N]) % MOD //i番目を選ぶ
初期値 †
- 探索がベースの DP はどこから始めれば全列挙ができるか考えると自然に初期値が定まる
- 初期値を定めることは探索ベースの時の関数呼び出しに相当する!初期値
- 初期値はDPの定義外.(そうじゃないと,空集合に対する場合の数みたいなのって扱われるべき?i=0, つまりAが空集合の時の場合の数が自明になる?A未満であることが確定している(j = 1)、「空集合」の元である自然数の場合の数は?→0A未満であることが確定していない(j = 0)、「空集合」の元である自然数の場合の数は?→1???本当に???みたいな悩み方をすることになる)
- ナップザックのような数え上げの問題では,初期値は0となる.
一方向に依存するDP †
- DPで漸化式が前にのみ依存している=ループを逆に回せば、後にのみ影響するDPを実現可能
- 一方向にのみ依存するDPは、用意する配列を1つだけに抑えることができる=漸化式が後にのみ依存している場合、i+1->iとして同じ配列を使いまわしていい(なぜかというと、DPの材料が必ず新鮮だから)
- d[i+1][j] = d[i][j]+d[i][j+1];
- i: 0 1 2 3 4 5
- 0: 0 2 7 5 3 2
- 1: 2 9 12 17 20 22
区間DP †
- 数列や盤面に対して、非常に典型的なDP
- 数列の典型区間DP dp[i][j] := [i, j]の区間での最大値(閉区間)
- 盤面の典型区間DP dp[i][j][k][l] := (j, i)(左上)から(l, k)(右下)の盤面での最大値(閉区間)
- 例えば50*50の盤面で、左上から右上に移動するパターンは2^100くらいあって無理ゲーだが、区間DPを使うと50^4となり現実的に
- 例題
- 数列: SRM 693 D1E
- 盤面: AOJ Stack Maze
- 盤面: ABC 8D
- 環状区間DP
- 「first枚目からcount枚の連続した区間の中から」みたいにやる
bitDP †
最後を全て持つDP †
挿入DP †
確率DP †
- 確率のDPは条件付き期待値を計算すると良い(つまり今までのことを考えてはならない!!!)
- これは、DPの遷移で、その和が必ず1になるように注意できるから。assertとかも最悪掛けられる。
- 656 D1E
- 確率DPは、未来が未知であることを加味した世界線を状態を設定しなければならない。「ここまででどういう状況で、未来は未知である」と表現する。
- 未来が確定した最終的な状態が境界条件となるので、メモ化再帰と相性がいい。
- 確率DPの遷移では、ある世界線での戦略は、その世界線から移動可能な世界戦となる。
- 確率の遷移は、遷移可能な世界線の確率と、足して1になるようなw_iによる内積となりがち
- 遷移は未来の固定(不確定要素を残した状態を確定していく過程となる)
未確定のDP †
問題特有の構造による状態削減 †
- yukicoder ドーナツ
- Rabbit Walking
包除原理のDP †
経路復元 †
- 動的計画法の復元
- 上記の方法の効率悪い部分を解決できる有力な方法は
- 各マスの値を更新するときに、ついでに、どのマスから伝播して来たかをメモしておく
- minのDPや最短経路長から、「最適な選び方」や「最短経路」や「最短経路の個数」や「辞書順最小な最短経路」を復元する方法。
- 各地点 v でゴールからの距離 d[v] を計算して、「e=(v,w) がゴールへの最短経路に含まれる道である <=> d[v] = (eの重み)+d[w] 」を利用して、貪欲に適切な道を選んでいけばいい
- 結論:以下の2つの概念を使うとDAG上の問題に落ちてDPができるようになったりする
- 最短経路DAG:最短経路として使われうる辺のみを残す。i->jの辺は、iにおけるjへの遷移が最適解として使われうる時に限り張る(D[j] = f(D[j], i->j))
- 到達可能最短経路DAG:最短経路DAGのうち、始点sから終点tへの経路として使われうるもの
- 到達可能最短経路DAGの必要性と計算方法
- 最短経路DAGだけでは、終点に到達しない可能性がある。
- なので、誤ったアルゴリズムとして、「始点sから最短経路DAGを辿って、終点tにたどり着けばよい」、みたいなのを考えがちだがこれはダメ。
- 到達可能最短経路DAGの構築は、最短経路DAGの逆辺グラフに対して、tから到達可能な辺のみ残すとできる。
- 経路のみ欲しい場合は?
- 到達可能最短経路DAGを構築するとDPができるようになって嬉しいが、実装重い。
- 始めからDP更新時に逆辺を張っておいて、終点tからDFSすれば必ず始点sに到達する(そこからスタートしたので)というアルゴリズムを組めて実装が軽くなる。
- DPでバグった時は、間違ってるところを見つけて経路復元したほうがよい。その場合全探索コードを書くこともできる
- ARC 32C 仕事計画
- 経路復元用の複数の情報を載せる(DP[i] = (x, y), xは時間yは次の最小位置)
- ARC 81 - E - Don't Be a Subsequence
- 具体的な構成の問題だが、まず最小値を求めるDPを書き、それの経路復元として構成を与える
戻すDP †
インラインDP †
- 例題: Code Festival 2019 Qual A - D
- 後ろから見ていく集める DP をすると分かりやすい
- 累積和を動的に求めていく方法は初めて見た(logかけてsegtreeで足しこんでいっちゃった)
戦略DP †
- 未来が不確定の場合、「iまで見て、その後最適解を行った場合の…」というようなDPになりがち
区間集合DP †
- 遷移が、「区間を取るか取らないか?取ったら、今見ている区間の最後までワープする」みたいになりがち
- ARC 32C 仕事計画
- Codeforces ??? D2D - My pretty girl Noora
制限付きDP †
- Codeforces 416 D2C(「座標iの右端にかぶる区間の左端がiを全て上回るような…」とかいう意味不明な状態を含める)
- SRM 653D1E 複数制限があるけど、初めにあたった制限のみを展開すると、再帰的に網羅できる。
連結DP - 接続関係のDP †
Monge †
- 性質の定義
- チョイス=minを与える遷移k
- チョイスの単調性=状態が増加するごとにチョイスも増加
- Quadrangle Inequality(QI) = 全ての\( i \le j \le k \le l \)について\( w(i, l) + w(j, k) \ge w(i, k) + w(j, l) \)であること
- Inverse Quadrangle Inequality(IQI) = 全ての\( i \le j \le k \le l \)について\( w(i, l) + w(j, k) \le w(i, k) + w(j, l) \)であること
- Monotone minima = \( w(i, j) \)の\( w(i, *) \)での最小値\( m(i) \)が単調
- Totally Monotone Minima = \( w(i, j) \)の任意の小行列について、\( w(i, *) \)での最小値\( m(i) \)が単調
- Closest Zero Point = \( w(i, j) \)を状態\( i \)のための遷移\( j \)による候補とすると、任意のxについて\( w(i, r) - w(j, r) \ge x \)なる最小の整数\( r \)を\( O(1) \)で計算可能
- DPと書くと目がチカチカするので式\( D_i \)とします
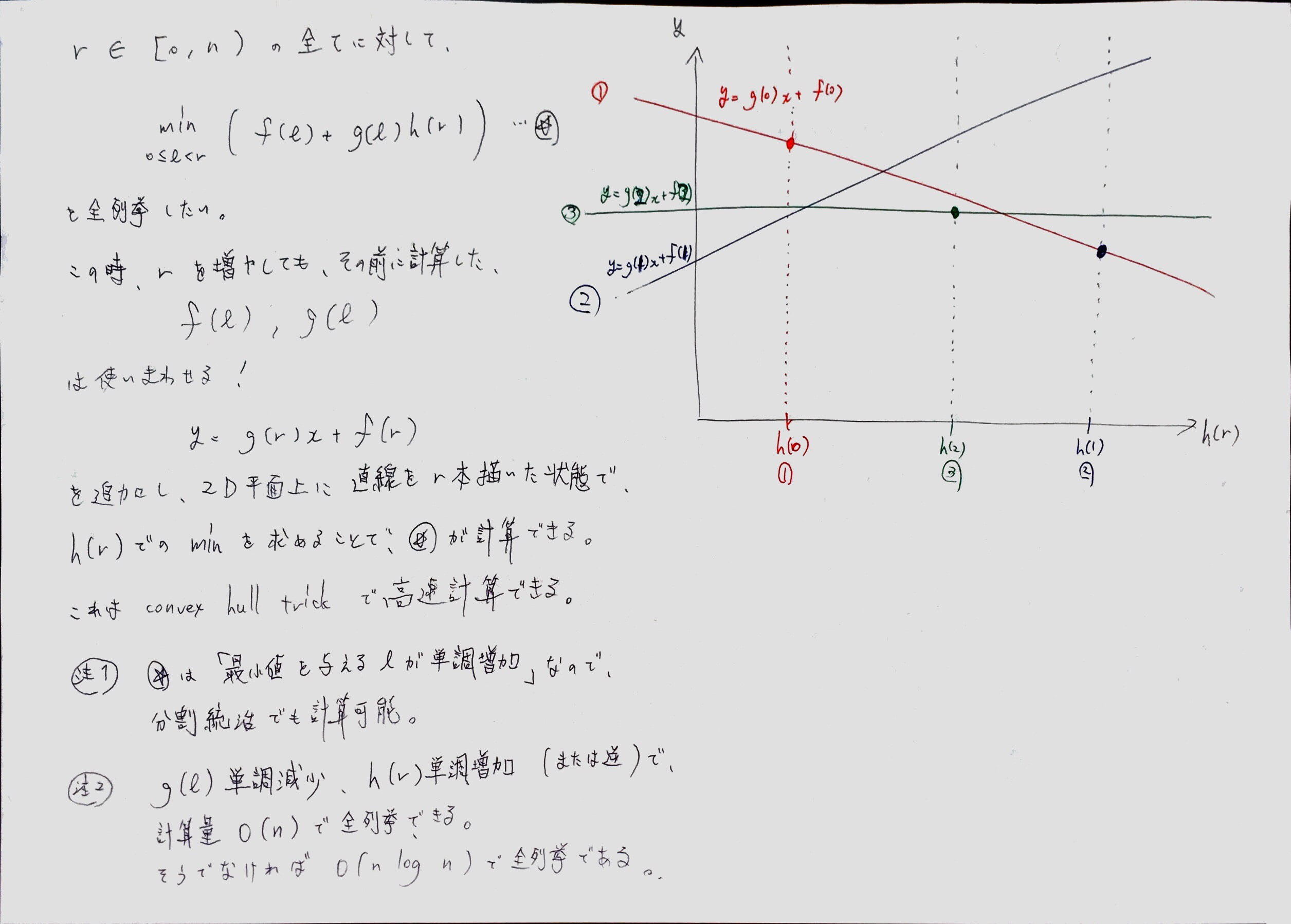
| 名前 | DP | 求める性質 | 高速化前 | 高速化後 | 例題 | 備考 | | Convex Hull Trick 1D | \( \displaystyle D_i = \min_{0 \le j < i}\ f(D_j, j)+g(i)h(j) \) | \( g(i), h(j) \)が単調でかつ単調性が逆 | \( O(n^2) \) | \( O(n) \)$ | p, p, p, p | | | Convex Hull Trick 2D | \( \displaystyle D_{i, j} = \min_{0 \le k < j}\ f(D_{i-1, j}, j)+g(j)h(k) \) | \( g(i), h(j) \)が単調でかつ単調性が逆 | \( O(k n^2) \) | \( O(k n \log n) \) | p(おすすめ), p, p | | | Divide and Conquer 0D | \( \displaystyle D_i = \min_{0 \le j < n}\ w(i, j) \) | \( w(i, j) \)がMonotone Minima | \( O(n^2) \) | \( O(n \log n) \) | | web、DPではない | | Divide and Conquer 2D | \( \displaystyle D_{i, j} = \min_{0 \le k < i}\ D_{i-1, k} + w(k, j) \) | wがQI(だと、チョイスが単調になる。すなわち\( A_{i, j} \le A_{i, j+1} \))。また、w(k, j)は区間拡大縮小さえ高速に計算できればよい。 | \( O(d n^2) \) | \( O(d n \log n) \) | p(おすすめ), p, p(尺取るコスト) | Convex Hull Trick 2Dで解けるものは全てこれも適用可能? | | Bar-Noy's Optimization | \( \displaystyle D_{i, j} = \min_{0 \le k < i}\ D_{i-1, k} + w(k, j) \) | \( w(i, j) \)がQIもしくはIQI。 | \( O(n^2 d) \) | \( O(n d) \) | | [6] まだ理解していない。Divide and Conquer 2Dの上位互換っぽい | | Knuth-Yao's Optimization | \( \displaystyle D_{i, j} = \min_{i<k<j}\ (D_{i, k} + D_{k, j}) + C_{i, j} \) | CがQIを満たす(すると、チョイスが縦にも横にも単調になる) | \( O(n^3) \) | \( O(n^2) \) | p | [1] | | Zvi-Giancarlo's Optimization | \( \displaystyle D_i=\min_{0 \le j < i}\ f(D_j, j)+w(j, i) \) | \( w(i, j) \)がQIもしくはIQI。 | \( O(n^2) \) | \( O(n \log n) \), wが更にClosest Zero Propertyを満たすならば\( O(n) \) | p | [2]、Convex Hull Trick 1Dで解けるものは全てこれも適用可能? | | Eppstein's Optimization | \( \displaystyle D_{i, j} = \min_{1 \le \hat{i} < i, 1 \le \hat{j} < j}\ f(D_{\hat{i}, \hat{j}}) + w(\hat{i}+\hat{j}, i+j) \) | \( w(i, j) \)がQI | \( O(n^4) \) | \( O(n^2 \log^2 n) \) | | [3] まだ理解していない | | SHAWK | \( \displaystyle D_i = \min_{0 \le j < n}\ w(i, j) \) | \( w(i, j) \)がTotally Monotone Minima | \( O(n^2) \) | \( O(n^2) \) | | [4], web |
- Convex Hull Trick, 1Dか2Dかわからないやつ
- [1] Donald E. Knuth. Optimum binary search trees. Acta Informatica, 1:14–25, 1971.
- [2] Galil, Zvi, and Raffaele Giancarlo. "Speeding up dynamic programming with applications to molecular biology." Theoretical Computer Science 64.1 (1989): 107-118.
- [3] Eppstein, David, Zvi Galil, and Raffaele Giancarlo. "Speeding up dynamic programming." Foundations of Computer Science, 1988., 29th Annual Symposium on. IEEE, 1988.
- [4] A. Aggarwal, M. M. Klawe, S. Moran, P. Shor, and R. Wilber: "Geometric applications of a matrix-searching algorithm", Algorithmica, Vol.2, pp.195-208, 1987.
- [5] L. L. Larmore and B. Schieber: "On-line dynamic programming with applications to the prediction of RNA secondary structure" Journal on Algorithms, Vol.12, pp.490-515, 1991.
- [6] A. Bar-Noy, M. J. Golin, and Y. Zhang: "Online Dynamic Programming Speedups", Theory of Computing Systems, Vol.45, No.33, pp.429-445, 2009.
その他 †
- CF438F
- Yao-Knuthは変更点が非常にすくなくてわかりやすいね。。K[i][i] = iで初期化してやるだけ
- いろんなパターン
- X(i) = min_{j<i} {
 j) + w(i,j) } 型のDPは,wがMongeなら O(n) で計算可能(これめっちゃすごいので是非勉強したい) j) + w(i,j) } 型のDPは,wがMongeなら O(n) で計算可能(これめっちゃすごいので是非勉強したい)
- X(i,d) = min_{j<i} {
 j,d-1) + w(i,j) } 型のDPは,wがMongeなら O(nd) で計算可能 j,d-1) + w(i,j) } 型のDPは,wがMongeなら O(nd) で計算可能
- f(i,j) がMongeのとき,「各 i について最小を与える j」を全部求めるのは O(n) で計算可能
- X(i,j,p) = min_{i≦s<j} {
 i,s,p) + i,s,p) +  s+1,j,p-1) } + w(i,j) 型のDPは,wがMongeかつ単調なら O(n^2 p) で計算可能(一般化Knuth-Yao 一般化ハノイの塔) s+1,j,p-1) } + w(i,j) 型のDPは,wがMongeかつ単調なら O(n^2 p) で計算可能(一般化Knuth-Yao 一般化ハノイの塔)
Mongeの気持ち †
- Mongeと行っているものは数学的に華麗だが、別に4角不等式はコンテスト中に証明できるものでもないので、DPのminを与える添字kがi, jについてともに単調、という表現で一般化したほうが実際の設計には役に立つ。
- minを与える最小のkをK[i][j]とする。mongeを考えるときは、f(i, j, k)のkを固定した2変数関数がmongeかどうかを議論する。minみたいなのが大事!もしgがあるなら、これはMongeかつ単調でなければいけない。個々別には、基本的には、Kテーブル上での不等式で考察することになる。
dp[i][j] = mink < j{dp[i - 1][k] + C[k][j]}一般的に
・K[i][j] <= K[i][j+1]・・・①
あるiで、jを動かした時に、kの探索範囲を減らせる具体的には、以下のように回せば良くなる。
dp[i][j]=min_{k \in [K[i][j-1], j)} (f(i, j, k))
でも、これでは最悪ケースだと、for all j K[i][j] = 0の時にO(n^2)、と思いきや、この性質+CがmongeでO(log n)に落ちる (分割統治法)
・f(i, j, k)がkについて凸関数
Kが上昇した時点で探索をやめて次に行くことができる。
でも、これだけでは最悪ケースだと、極小値がめっちゃ奥にあるケースでO(n^2)、と思いきや、3分探索することによってO(log n)に落ちる
dp[i][j] = mini < k < j{dp[i][k] + dp[k][j]} + C[i][j] このケースに限定
・K[i-1][j]<=K[i][j]<=K[i][j+1]
これが満たされているだけで、計算量が落ちる。
DPテーブルを斜めに埋めていく(要するに、区間[i, j)の長さlenに関して小さい順に埋めていく)ことができる。min_[k \in [K[i-1][j], K[i][j+1]] (f(i, j, k))
満たされているかどうかの直感的なチェックは、[i, j)の区間を広げたり狭めたりするとわかりやすい
数学的なチェックは、a<=b<=c<=dについてC[a][c]+C[b][d] <= C[a][d] + C[b][c]かつC[b][c] <=C[a][d]ならば、上の条件が満たされる(十分条件)。また(f*g)(i,j) := min{i≦s<j} { f(i, j) + g(i, j) }は、f, gがmongeなら
dp[j] = mini < j{dp[i] + C[i][j]}
CがmongeならばO(n) http://codeforces.com/blog/entry/8219#comment-139241
Monotone minima †
- 「行ごとの最小値の配置が(行列として見たとき)右下に単調に下がっていく」(重要!というかこれが本質)
- totally monotone minimaはそれの強いバージョン(部分行列に限ったとき,その中の行最小値配置が単調)
- mongeならばTM(逆は不成立)
- KYスピードアップと、TMスピードアップというものがある。しかし、Bein-Golin-Larmore-Zhang(2009)でKYできるならTMできることが示されたので、アルゴリズム的には大して変わらない
- KYとTMによるアルゴリズムのちがい
- Monotone minimaならO(m log n)でできる。これが所謂分割統治と言われているやつ
- TMMinimaなら、SMAWKアルゴリズムでO(n+m)でできる。
- どんなやつがSMAWKかというと、「最近点問題」の特殊版
- 入力:平面上の点集合 P, Q,ただし P は x 軸上に乗っている
- 出力:各 p ∈ P に対する最近点 q(p) ∈ Q。f(p,q) := d(p,q) とおくと,
- P, Q が x 座標でソートされているとき,f は Totally Monotone となり,したがって SMAWK が適用できます.
- (Not tottaly) Monotone Minimaの時はa[i][j]<a[i][j+1]が満たされているとは限らないが、四角形2つを分割するD&Cになる。tozanさんのスライドも同様。
- 何が言いたいかというと、D&CはSMAWKの前の奴とa[i][j]<a[i][j+1]のやつで2つある
- こないだのD&Cでのコストが具体的に計算どうするのか(結論、あのD&Cはコストが左右両方に尺取りO(w)で(n w log n)が行ける)みたいな計算論的な問題もあってですね。
- Monge(O(n^3)->O(n^2))<Totally monotone(SMAWK, O(mn)->O(m+n))<Minima(O(mn)->O(m log n))
という構造
- Monge.cppを、Monge, Totally Monotone, Monotone, n!=m,の性質と、何が使えるか(SHAWK, 分割統治、KY Speedup)をきちんと整理して出すようにする
- f(i,j) がMongeのとき,「各 i について最小を与える j」を全部求めるのは O(n) で計算可能( A. Aggarwal)が、SHAWKのこと
- mongeの重要なポイント!DPテーブルの一番端っこが埋まっていること!つまり、DP[n][n]であること。なぜかというと、DPから外れたところの上限を参照し始めてしまうから。つまり、mongeで高速化される領域はDP[n][m]の場合にはmin(n, m)^2にしかならない!
不思議なDP高速化 †
- Codeforces Round #422 (Div. 2) D. My pretty girl Noora
- AtCoder? ARC 44C - ビーム
- 自明DP O(HWW)
- これを以下によって改善すると
- マンハッタン距離を局所的に見ると近くで距離1
- ビームが飛んでくる数が疎
- 時刻0.5の状態を作る
- 改善DP O(Q)
- 遷移
DP[i+0.5][j] = DP[i][j] (時刻iで座標jにビームがこないなら)
DP[i+0.5][j] = min(DP[i+0.5][j], DP[i+0.5][j-1]+1) (時刻iで座標jにビームがくるなら)
DP[i+0.5][j] = min(DP[i+0.5][j], DP[i+0.5][j+1]+1) (時刻iで座標jにビームがくるなら)
ビームが来ない遷移がQW-Q回と大量に行われることに着目すると、DPテーブルを使い回すことによってO(Q)で上記の遷移を実装することができる。
また、DP[i+0.5]からDP[i+1]への遷移はビームが来る場所が行けないというだけなので、
DP[i+1][j] = INF (時刻i+1で座標jにビームがくるなら)
DP[i+1][j] = DP[i+0.5][j] (時刻i+1で座標jにビームがこないなら)
- Code Festival 2017 予選C D
- 条件を集合の演算にしてminを入れ替えると、漸化式の中に漸化式が出てきて高速化される
状態と格納された値を交換するテク(min, max) †
DPではない †
- DPのように見えるが、さらなる高速化のためには考察が必要な問題
典型 †
- 部分集合を全列挙するbitDPはO(3^n)である
- 理由は(1+2)^nの二項展開を考えると自明
- ちなみにO(4^n)は自明。\( S \)を\( O(2^n) \)で固定する。\( i \cup mask \)なる\( i \)を\( O(2^n) \)で全列挙すればよい。
# jのループが、iの空ではない部分集合を全列挙している
int dp[32768]={0};
rep(i,1<<n)for(int j=i;j>0;j=(j-1)&i)dp[i]=max(dp[i],dp[i^j]+mazeru[j]);
# jのループが、iの全部分集合を列挙している(雑だけど)
int dp[32768]={0};
rep(i,1<<n) {
bool first = 0;
for(int j=i;j>=0;j=(j-1)&i) {
if (j == 0 && first) break;
if (j == 0) first = 1;
dp[i]=max(dp[i],dp[i^j]+mazeru[j]);
}
}
関数DP †
- 状態に連続値が入る場合、関数を持つ必要がある (ARC 72F)
最小値のDPは遷移をサボれる †
- DPはお気持ちが大切と思ってる立場としては、「組み合わせの個数を求めるDPと、最大値を求めるDPの、決定的な違いはなんですか?」というのを割と考えてほしいなぁとよく思ってます(この辺は記事にするつもりでめんどくなってやめた)
- 組み合わせは、「辺が切れる」ってのがあんまりないんだけど、最大化・最小化は「辺を切る」ってのが出来ることが結構多い
- こうなんか、数え上げだと「この遷移を考えるのは無駄」みたいなのは絶対ないんだけど、最小化だと「この遷移は考えなくて良い」みたいなのが大量発生する、みたいな。
- dp[i][j]=min{dp[i-1][k]+L[k] | j<=k}+R[j]みたいになるL,Rがあるなというところからスタートするとよさそう、逆方向にもう一本式があるけど
- 実家処理として
遷移をくくり出すことによるDP高速化 †
- なんか遷移がk個あって混み合っている場合、k=0をくくり出すと高速化されるケースがある
- 例\( D_{i+1, j} = \max_{0 \le k} D_{i,j-k w_i} + k v_i \)
- \( = \max_{1 \le k} (D_{i, j}, \max(D_{i, j-k w_i}+k v_i)=\max_{0 \le k} (D_{i, j}, \max(D_{i, j-k-1 w_i}+k v_i)) \)とくくり出す
- すると、\( D_{i+1, j} = max(D_{i, j}, D_{i+1, j-w_i}+v_i) \)となり、計算量が落ちる。
- 蟻本 - 重複組み合わせ、も同じ方法で計算量が落ちる
遷移の中のmin, maxの単調性 †
- \( D_{i, j} = \max_{0 \le k<i}(D_{i-1, k} + \min(x, a_j-a_k)) \)
- minでどちらが選ばれるか?に対して、kが単調。したがって、\( x>a_j-a_k \)となる最小の\( k = m \)を事前計算しておくことで、RMQで解けるようになる。
DP内DP †
集めるDPと配るDPの変換 †
使い回すDP †
循環するDP †
環状に循環参照しているDPの更新は、何周か愚直に更新すればいいことがあるわ。例えば、dp[0]=min(dp[0],dp[1]+1),dp[1]=min(dp[1],dp[2]+1),...,dp[k-1]=min(dp[k-1],dp[0]+1)という操作を同時にやりたい場合は、k-1から0の順番に2周して更新すればいい。
Priority Queue †
- クエリ突っ込みながらソートしたい!という時のため。
- これだけだと、二分探索木(STLのmap)もできるが、これはもっと静的でクエリ解消はできない
- priority_queue
- 何も指定しないと最大がtopになる。普通のソートとは直感が逆なので注意。
priority_queue<ll, vector<int>, greater<int>> q; // topが最小
priority_queue<ll> q; // topが最大
- デバッグ
- 出力は、イテレータが使えないので、コピーして全部取り出さないといけない。auto q_tmp = q; while (!q_tmp.empty()) {cout << q_tmp.top() << " "; q_tmp.pop(); } cout << "#" << endl;
マンハッタン †
- 「45度回す」!!!!!!!!!!!!!
- 典型中の典型
- 一般に,「解は必ず存在することが示せます」と書いてある問題はパズルゲーであり,解法が鮮やかであることが知られてゐます。大きいやつで一例あげましょう
- Code Festival 2017 Qaul A - B問題?
最小辺カバー †
FFT †
FFT †
- 結構自然な問題
- 添字の順序の総和が一定となるような掛け算の総和は、O(n log n)で計算できる!
- 用途
線形漸化式と畳み込み †
NNT=高速余剰環畳み込み †
- コード
- mod pでの畳込みはO(n log n loglog n)で計算できる。
- 実は任意の余剰でもO(n log n)でいける。
- p=2の場合、特に高速XOR変換と呼ばれる。bitsetが使えるなど、定数倍を早くできる。
- NTTの別名
- 高速剰余変換 O(n log n)
- 高速xor変換 O(n log n)←法が2の時はこうも呼ばれる。適切な演算子が使えるので定数倍が高速
拡張ダイクストラ法 †
誤差 †
浮動小数点 †
- 例えば、(ll)pow(3, 3) = 26
- とにかく浮動小数点は誤差が出る。
誤差の減らし方 †
- 誤差が厳しい場合
- long doubleを使う
- ハフマン符号のように小さい数値から足していくだけでも誤差減る
「long longのcastで大きくなる」誤差 †
- 前提として丸め誤差は大きくなる
- doubleの精度が15桁であるが、17桁を扱おうとするなどしたら起きる誤差
- 本当の答えが0.999999999999とかである時、丸め誤差が発生すると1.00000000000001とかになる。
- long longのキャストせよという問題なら、本当は0であるべきところが1になる。
- yukicoder 413
double型行列はヤバい †
- 絶対値が3以下くらいでも、long doubleで15乗くらいしかできない
- 理由: 掛け算と足し算が混在し、3^15で計算誤差がdouble型を超えるので
Wavelet Matrix †
- AlgoogleさんのWavelet Matrixの実装
- 簡潔データ構造
- 簡潔データ構造とは、データ構造を最適に近いサイズで保存しつつ、インデックスを利用して高速な操作を実現するデータ構造のことです。
- 情報理論的下界に「近い」領域量を使ったクエリデータ構造
- 要するに空間計算量が小さくて、実際にそういう実装をするという意味(本当の定義はもっと厳密だが)
- 簡潔データ構造の種類
- bit列に対して→完備辞書=簡潔ビットベクトル
- Wavelet MatrixやLOUDSはこれを使って実装するので重要
- 数列に対して→Wavelet Matrix
- 特にquantileクエリがすごい([l, r]のK番目の数字は?)
- 木に対して→LOUDS
- クエリ
- quantile
- rankLessThan
- k-th reduce
- [l, r)でk-th以内の値を全てopしたら?
- 各bitベクトルで、bitが0の部分に単位元を突っ込んだseg木なりいもすなりSparseTable?なりをO(log m)個構築する。あとはこんな感じで
- opが+, -など全域に渡って群ならば、いもすを載せる。雑な実装でO(log m)
- opがmax, minならば、SparseTable?を載せる。雑な実装でO(log m log log m)
- opが0を含む掛け算など逆元が存在しない場合は、Segment Treeを載せる。雑な実装でO(log^2 m)
- 順位と演算対象が異なる場合は、まだよくわからない
- 重複除去した範囲種類クエリ
- colored range counting / reporting という名前
- 完全動的Wavelet Matrix
- FIDを平衡二分探索木で実装することでinsert/erase/rank/selectをO(logN)で実行できます
- これでwaveletmatrixを構築すれば、updateはeraseとinsertで実現可能です
- これで動的quantileできる。
- ちなみに完全動的WMは
- 長さNの数列があって、indexを指定して値を挿入する操作です(長さはN+1になります)
- 動的waveletmatrixはsplit/mergeも不可能。これは二段目以降でindexが混ざってしまっていることに起因しています
Subset Convolution †
- クロネッカー積、バタフライ演算から、高速ゼータ・メビウス変換を導いてる。すごい
背景 †
- 集合\( S \)、集合\( S \)の\( i \)bit目を\( S[i] \)とする。
- 命題\( P(i) \)がある。
- 例えば\( |S| = 4 \)とする。
- この時、以下の\( 3^4 \)個の命題\( P(c_1 c_2 c_3 c_4), c_i \in \{0, 1, ?\} \)が定義する。
- \( c_i=1 \)は、\( P(i) \)が必ず満たされていなければならないことを表す。
- \( c_i=0 \)は、\( P(i) \)が必ず満たされてはいけないことを表す。(これが重要)
- \( c_i=? \)は、\( P(i) \)についてはどうでもいいことを表す。
- \( P(c_1 c_2 c_3 c_4) \)に対応する「\( P(a, b, c, d) \)が満たされる時の場合の数」といった群への関数\( H(S) \)が定義できる(群なら場合の数じゃなくてもいい)
- 例
- \( P(10?1) = P(0) \land \lnot P(1) \land true \land P(3) \)
- \( P(1111) = P(0) \land P(1) \land P(2) \land P(3) \)
- \( P(1?10) = P(0) \land true \land P(2) \land \lnot P(3) \)
- \( H(1?11) = the\ number\ when\ P(1?11)\ is\ satisfied \)
- ここでやりたいことは、「一部のH(S)から、他のH(S)を復元したい!!」
- 結論からいうと、以下が計算可能(ただし、実装に置いて添字がちょうどこの説明と対応しているとは限らない!)。
- 「?がないSについて、H(S)が全て既知」→「0がないSについて、H(S)を計算」(高速ゼータ変換。\( O(n 2^n) \))
- 「0がないSについて、H(S)が全て既知」→「?がないSについて、H(S)を計算」(高速メビウス変換。\( O(n 2^n) \))
- ここでのH(S)において、T=「Sの?を全て0に置き換えた集合」とした時、普通H(S) = g(T)と表記する(普通)。
- 「0がないSについて、H(S)が全て既知」→「0を含みうる制限のないSについて、あるH(S)を計算」(包除原理\( O(2^n) \))
高速ゼータ変換 †
- dp[i]=a[i]; となってるときに高速ゼータ変換を適用すると、iの部分集合に対応する数jすべてに対する値dp[j]を"まとめた"値がdp[i]に格納される。まとめ方をmaxにすれば部分集合に対するmaxが取れる
- ex) dp[] = {3, 1, 4, 1, 5, 9, 2, 6}
- dp[] = {3, 3, 4, 4, 5, 9, 5, 9}
- dp[6] <- max{dp[0],dp[2],dp[4],dp[6]}
S=0100が2個
S=0001が3個
S=0011が4個
その他は0個である。
この時、
S=???1の総数は?→7個
S=?1?1の総数は?→0個
S=?1??の総数は?→2個
- 高速ゼータ変換は環で動く(+, *, max, gcdなど)
高速メビウス変換 †
- 典型的には、「積集合の値を、厳密な積集合の値に変換する」という用途で使われる。
- どういうことか?
- 積集合の集合Sの全ての条件を満たしていればいい。
- 逆に言えば、全体集合-集合Sに含まれる条件については、何も考えなくてよいということ=?に相当している。
- 曖昧な?ではなく、厳密に満たされない'0'での場合の数を計算することができる。
- AOJ 2446 Enumeration
- \( P(i, n) \) = \( a[i] \)で割り切れる
- \( P(S, n) \) = \( P(S_0, n) \land P(S_1, n) \land ... \land P(S_{n-1}, n) \)
- \( g(S) \) = 1からmに含まれるnについて、\( P(S, n) \)が満たされる場合の数
P(S=??11)、つまり「a[0]についてはどうでもよく、a[1]についてはどうでもよく、a[2]で割りきれて、a[3]で割り切れる」場合の数、g(S)個
P(S=1??1)、つまり「a[0]で割りきれて、a[1]についてはどうでもよく、a[2]についてはどうでもよく、a[3]で割り切れる」場合の数、g(S)個
...
上記の情報から、以下を計算する。
P(S=0011)、つまり「a[0]では割り切れず、a[1]でも割り切れず、a[2]で割り切れて、a[3]で割り切れる」場合の数
P(S=1100)、つまり「a[0]で割りきれて、a[1]で割りきれて、a[2]で割り切れず、a[3]で割り切れない」場合の数
...
2種類の高速ゼータ変換 †
- 高速ゼータ変換には2種類の実装があってconfusing(なんか立式との整合性が合っていなかったりするし。)
- iwiwiさん形式
rep(i, n) rep(b, 1 << n) if (!(b & (1 << i))) chmax(dp[b], dp[b | (1 << i)]);
集合Sが与えられた時、Sが含むもののreductionを計算
rep(i, n) rep(b, 1 << n) if (b & (1 << i)) chmax(dp[b], dp[b ^ (1 << i)]);
集合Sが与えられた時、Sを含むもののreductionを計算
包除原理 †
S=0000の総数は?
return dp[????] - (dp[1???] + dp[?1??] + dp[??1?] + dp[???1]) + (dp[11??] + dp[1?1?] + ...) - (...
平均値と中央値の関係 †
文字列操作 †
文字列でやりたいこと †
- sが大きな文字列、t_iがマッチングする文字列, |s|=n, |t|=m
- 0-index LCP
- sとt_0の最長共通文字列長を求める
- 重要なのは、マッチング文字列は1つに限定されているということ
- i-index LCP
- sとt_0, t_1, ..., t_nの最長共通文字列長を求める
- マッチング文字列は複数指定可能
| 名前 | 構築 | 0-index LCP | i-index LCP | contain | | SA-IS | O(n) | O(1) | O(1), RMQにメモリ削減のためSegment TreeならO(log n), 複数個の文字列のマッチングが可能 | O(log n) | | Rolling Hash | O(n) | O(log n) | O(log n), 複数個の文字列のマッチングが可能 | 不可能 | | Z-Algorithm | O(n) | O(1), 1個だけの文字列のマッチングが可能 | 不可能 | 不可能 | | boyer moore | なし | 不可能 | 不可能 | 最悪O(n), 平均O(n/m) |
int getLCP(int i, int j)の使い方 †
- SA-ISとかZ-Algorithmを見て、「sa.getLCP(i, j)とか言われても、これでどうやって文字列sと文字列tのLCPを求めるんだ…」と思うこと必至
- int getLCP(int i, int j)の挙動
- saの構築にsを用いたとすると、s[i:end]とs[j:end]の最長共通接頭尾長を求める。
- え、tどこいったの?と思う
- で、どうやってマッチングするの?→t+sに対して構築する!
- saの構築をsa(s)ではなく、マッチング対象t1, t2があったとしたら、sa(t1+t2+s)として構築する。
- こうすると、sa.getLCP(0, |t1|+|t2|)とすることで、t1とsのLCPを求めることが出来る!
boyer moore search †
回文 †
MP †
- 0からの回文をO(n^2)ではなくO(n)で全列挙できる!
- MP
- O(n)で、文字列 S が与えられたときに、各 i について「文字列S[0,i-1]の接頭辞と接尾辞が最大何文字一致しているか。ただし|S[0,i-1]|未満の一致とする。」を記録した配列を計算。
Manacher †
- Manacher
- 各 i について「文字 i を中心とする最長の回文の半径」を記録した配列 R を O(|S|) で構築するアルゴリズム
ローリングハッシュ †
- h(0, i)=h(0, i-1)*b+s[i] で定義される文字列のハッシュ。
- 何が嬉しいかというと、このハッシュは群的なので、h(j, i)がh(0, i)からO(1)で計算可能
- 「iから長さkと、jから長さkのLCP」が構築O(n)クエリ(log n)で計算できる。
- modとbaseをランダムにしないとhackされる
Zアルゴリズム †
- 「0から長さn-jと、jから長さn-jのLCP」が構築O(n)クエリ(1)で計算できる。
- 資料
- 例題
- AOJ Almost Same Substring
Suffix Array †
- できること
- iとjから始まる文字列からのLCSクエリO(log log n)
- ただ、MLEが怖いのでSparse Tableではなく、Segment Treeで実装することが多い。それだとクエリO(log n)
- ある文字列が含まれているか?containクエリO(log n)
- いろんな構築方法(普通にSA-IS使いましょう)
- Suffix Array 構築O(n^2 log n)=比較O(n)*ソートO(n log n)
- multikey-quicksortなるものを使うと早くなるらしい
- SA-IS 構築O(n) (Two Efficient Algorithms for Linear Time Suffix Array Construction [G Nong, et.al.]) 2012年現在最速
- Manber&Myers : 構築O(n (log n)^2) プロコン的にはよく使われる、上の記事はこれ、コメントいっぱいついてる
- Larsson-Sadakane O(n (log n)^2)) ← spaghettiのやつ
問題集 †
Trie †
- 最長接尾辞パターンの多分木(256分木)
- XORクエリの最大化でも使える
KMP, Aho-Corasick †
- 結局、KMP⊂Aho-corasick
- KMP法 : 単一文字列のマッチングアルゴリズム
- Aho-Corasick法 : 複数文字列のマッチングアルゴリズム
- Aho-CorasickはCovering Matchingバージョンに簡単にすることができる
- マッチングしたノードの失敗編を全てrootに張り替えることによって。
- マッチングの微分が求まるので嬉しい(=入力文字列の1文字1文字に対してマッチングいくつふえたかが分かる)
- グラフの頂点bitmaskを遷移していくと、やたら状態数が少ないので250bitのbitDPが数ms(Topcoder 709D1M)
- 直感的には、素数ループの周期数が限度?とすると250頂点あり得りそう
- 2*3*5*7*11*13*17*19*...*41 (和が238) = 3e14くらいあるはずなので、やばそうなのだけど。
- たくさんbitはあるけど、「同時には出ない」みたいな制約とか、遷移が少ないと出切らない、みたいな感じなのだろうか。
- 例題
k-mismatch-matching †
- k個未知の文字列"he?lo wor??"が、もう片方の文字列に含まれているか
- SA-ISでO(k n)で解けるはず。AOJ Almost Same Substring講評参照
Tutte行列 †
- やるだけのやつが有るらしい
- Sunny Graphでも使えるらしい
Suffix automation †
一般マッチング †
- 復元しなくていいなら、一般グラフの最大マッチングは行列補間がラク
- 行列補間は、一瞬グラフの最大マッチングに限らず、他にも色んの問題を解けるテクなのん。
- 行列補間を特に一般マッチングに適用するときに登場する行列を Tutte 行列と言うのん。
- 何度もごめんなのん。
- ウチが行列補間と言ったもの、蟻本では Tutte 行列と書いてあるのん
- 行列補間は、一瞬グラフの最大マッチングに限らず、他にも色んの問題を解けるテクなのん。
- 行列補間を特に一般マッチングに適用するときに登場する行列を Tutte 行列と言うのん。
- 例題
- Garbow's Edmonds Algorithm speed upというアルゴリズムが一般マッチングで超早いらしい
辞書順 †
- 同じ桁なら、数字比較と辞書順比較が数字比較で一致する
- 辞書順は最近のものを26分木でまとめていくと辿れる(TDPC G)
連続部分列 †
二分木 †
- 追加も削除もある場合の頻出テクは、クエリの(平方)分割かがんばって動的になんとかするですが、動的のほうを扱います。
- やりたいことは「ソートしながらデータを持つ」データ構造
- できること
- insert(k, x): k番目に値xを挿入
- erase(k): k番目の値を削除
- merge(l, r): l+rをする
- split(l, k): [0, k)と[k, n)の2つの列に分解
- 値に関する質問・更新: sum, addなど
- insert/eraseベースと、merge/splitベースの2つがある。どちらかが実装できると、もう一方は超簡単
動的木の基本発想 †
4
2 3
4 5
- 列aと列bをくっつける操作a+bを、木と木をくっつける操作として実装する。
平衡 †
- 基本だと、1,2,3,4,5,...,nの入力でなんかヤバくなる
- どんなものが平衡二分木?
- 赤黒木(std::map)、スプレー木(Link-cut Treeに使う。ならしO(log n)だが最悪時間O(n)なので注意)、Treap、AVL木、くらい覚えとけばよさそう
- 平衡
- 左右の深さが偏らないように回転 (rotation)
- 回転=順序を保存したまま木構造を変形。
- 順序を保存=同じ順序関係を表す二分木であるという意味。参考(111ページ)
- Left Rotationが左を下げること、Right Rotationが右を下げること。
各論 †
- いろいろな平衡木がある
- Treap: キーと一緒に「優先度」を持つ。キーを見ると二分探索木、優先度を見ると二分ヒープ(常に親が子より大きい)になるように木を構成
- Splay: 2つ親までを見れば、回転によって平衡化が可能なことを利用した平衡木。頂点xを根の場所まで移動させてできる木を返す
- RBST: l+rの時、l/l+rの確率でlを根にするとなんとならしO(log n)
- 赤黒木: 定数倍が早い
RBST †
- merge
- mergeの仕方には左右があるので、それをランダムに選ぶことによってならし\( O(\log n) \)を実現
- l+rの時、l/l+rの確率でlを根にするとなんとならしO(log n)
- split
- 切れる部分になったらreturnして、それ以外は掘っていくことで可能 これ, antaさんのRBSTで、yosupoさんもsplitでの境界条件をこんな感じにするテクニックを使っていたから定番らしい(どうやら、子供がいない場合にNULLではなくnullnodeというnullみたいなノードにポインタを指すせることでいい感じにやる方法らしい)
Euler Tour Tree †
その他勉強用情報 †
- 永続平衡二分木はpekempeyさんがよさそう
- 永続での検索
Link Cut Tree †
- Link-cut Treeのなりたち(下に行くほど実装が重い)
- 頂点vから根へのパスをつなげる(expose, 必須で平衡二分探索木のsplit, mergeを使う)
- 頂点の親を変更(link)、削除(cut)
- 木の根を求める(root), 木の根を変更(evert)
- パスに対する頂点・枝の値のクエリ(sum, max, 更新)
- コンセプト
- ツリーを分解してパスにします。
- パスをsplay木で管理します(パスの順序さえあってればいいので、根は自由に選べる。よく実線をsplay木内部の辺、点線をsplay木間の辺として表記する)
- 辺更新は u→v という辺を張らずに、u→e→v のように間に辺のノードを挟んでおけば簡単!!!!
- 歴史
- 1983年段階で、密グラフのフローはO(n^3)が最速(V. M. MALHOTRA, M. P. KUMAR, 1978)、疎グラフでは1980年のO(E V log^2 V)(Z. GALIL AND A. NAAMAD)しかなった。
- Link-Cut Treeを利用してDinits(ロシア人なので表記ゆれがあるがDinic。Dinitz's Algorithmとも呼ばれたりもする。1970年)のmax flowアルゴリズムを改善することで、O(E log V)を得た(1983, Sleator, Tarjan)
- まあ、maxは半束で少なくとも可換モノイドで代数学的に強いデータで考察されていたが、慎重に扱うと一般のモノイドについて扱うことができる。
Euler-Tour Tree †
- Euler-tour treeとLink-cut treeは同様に神がかり的木
オフラインクエリ †
- オフラインクエリに関するDecomposable searching problem
SAT †
2-SAT †
- 2-sat問題
- 「命題iが満たされるならば命題jは満たされない」とか「AとBが同時に成り立つことはない」といったルールが大量にあるときに、全部のルールを守ることができるか?という問題。
- 全i, jについてルールを記述する必要があるので、せいぜいn<2000くらい。
- どうやって解くかというと、A⇛Bを有向グラフとして、A⇛¬Aになったらアウトなので、SCCで同一成分になってるとダメ
- 2-SATの説明わかりやすい
3-sat †
- NP困難だが、10^6くらいまで高速に解く方法がある
- togasatでは3000くらいまでならいける
SATの範囲クエリ †
- for all t, \( x_s \)->\( y_{t \in [i, j]} \)の辺を張る、というのはSegment Treeの要領で辺を作ってしまえば良い (ARC 69F)
対称性の利用 †
- 対称ならばx>=yのようにしても問題ない
- 実装が簡単になる可能性がある
- 左右両方から探索する場合、配列をreverseして全探索すれば良い。
- 左右対称を利用して状態を削減することができる場合もある
- 左右独立の典型
- CF505D1D 区間DPをO(n^5)からO(n^3)まで落とすやつ。左右独立で遷移をO(n)落とし、左右独立なので片方だけを状態に持つで状態をO(n)落とす。
ゲーム †
解き方の大まかな分類 †
- 深さ探索するもの
- 状態列挙してGrundy数を使うもの
- ゲーム特有の性質を使うもの
猿真似 †
- ゲームのパターンに相手を真似するというのがある
- これをやると対称性が敗れる時のみに考慮すべきことを短くすることができる
WL-Algorithm †
- DFS必勝法。stateが先手必勝かそうでないかを全盤面に割り当てる
- まず明らかな勝利条件はすぐにreturnしておいて、
- 「盤面sで先手必勝」⇔∃a in action s’=T(a, s) and dp[s’] = 1 相手に後手必勝を押し付けられる。
- 「盤面sで後手必勝」⇔∀a in action s’=T(a, s) and dp[s’] = 0 何やっても相手に先手必勝を渡してしまう
- 勝利で終了が定義されているWL-DPでは、「このような手で渡されたということは、直前の人が勝ったのか、ということは俺が負けか」みたいな感じで敗北を吐いて死ね
boolean isWinning(State pos){
State[] nextStates = { posから到達できる全ての次の状態 };
for(State s : nextStates){
if(!isWinning(s)) return true;
}
return false;
}
- このタイプの理解の方法
- 二つの状態の定義があり、この曖昧さによって混乱が生じる!どちらの立場なのかをきちんと明確にすること。
- 勝ち状態wを「この状態から始めた人は必ず勝つ」、負け状態lを「勝ち状態ではない」と定義する。(こっちのほうが一般的!)
- 遷移は、「次に負け状態を相手に押し付けられる遷移が選べるならば勝ち」=「遷移先にlがあればw, なければl」
- 勝ち状態wを「この状態で終わっ人は必ず勝つ」、負け状態lを「勝ち状態ではない」と定義する。
- 遷移は、「終わったあと、勝ち状態を相手が選べてしまうなら負け」=「遷移先にwがあればl, なければw」
- 基本的には、「始め」の勝ち状態のほうを、一般的に勝ち状態と言う。
- 勝ち負けゲームの定番解法「勝ち状態にwを置いて、負け状態にいけないなら負け、負け状態にいけるなら勝ち」
- rngさんのAGC02 E問題の解説(youtubeに上がっている)を見るとわかりやすい
- AさんとBさんが違う目的に向かう場合
- 例: TCO 2018 R3A Easy
- こういうのはちゃんとターンごとに決めてかないといけない
- AさんでもBさんでもどっちでもよいのだが、後ろから敗北条件・勝利条件を伝播させていく
- この場合、Aさんの条件とBさんの条件が異なるので、ターンごとに場合分けをしていかなければならないし、「Aさんのターンで、状態がsであるような場合にBさんが勝てる」みたいにターンを明示的に状態に含む必要すらありえる。
ゲームの分類 †
- 二人
- 四人(麻雀)
- 二人(将棋・囲碁・オセロ)
- 一人(ソリティア)
- 有限
- 有限回で終わるゲーム
- ゲーム木(=局面全体を頂点集合とし、局面Pから局面Qに移動できるとき、PからQに矢を作って得られるグラフ)において、どの頂点から始まる有向パスの総数も有限
Grundy数 †
- pekempeyさんの良い解説
- 定義
- mex(S) = 集合Sに含まれない最小の非負整数(空集合に対しては0)
- Grundy数が負けの状態なら0とする
- 負けの状態ではないGrundy数は、mex(遷移先)とする
- 現在の状態の Grundy 数が 0 なら後手必勝、そうでなければ先手必勝。
- 何がすごいの?
- 複数の山がある場合のGrundy数は、g(a,b,c)=g(a)⊕g(b)⊕g(c)。
- 山ががある場合のGrundy数は、g(a,b,c)=g(a)⊕g(b)⊕g(c)。
- 山が分裂する場合のGrundy数は、g(n)=mex(g(n−1),g(n−2),g(n−3),g(x1,x2,…,xn))=mex(g(n−1),g(n−2),g(n−3),g(x1)⊕g(x2)⊕⋯⊕g(xn))
- g(n-1)からg(n-3)は、Nいっちゃダメゲームで1から3だけ減らせる時のGrundy数を表す。g(x1,x2,…,xn)は分裂後のGrundy数を表す。
- 性質
- Grundy数は「遷移可能な状態の個数」で上から抑えられる
- そのゲーム特有の Grundy 数の性質を見つかる場合あり。N言っちゃダメゲームの場合、単にmodを取ればGrundy数が求まる
- 拡張性
- もちろん、Nいっちゃダメゲーム以外にも使える。
- 具体的には、状態遷移図がDAGなら使える
分裂するgrundy数 †
- 集合Sがある。n in Sに対する操作はq_n個存在する。操作i「数nを消去し、{x_{i, 1}, x_{i, 2},... x_{i, m_i}}を追加する」もしくは操作-1「数nを消去する」。集合Sの任意の数について、任意の操作を行えなくなったら敗北である。この時、先手必勝か?
- 数nのgrundy numberをg_nと定義する。集合Sのgrundy numberはg_Sと定義する。f(n, i) = nに操作iを行った結果に得られる数の集合と定義する。すると、
- 数nを消去すると、数がなくなってそこから操作ができず負け状態なので、f(n, -1) = {0}
- 数nに操作iを行うと、f(n, i) = {x_{i, 1}, x_{i, 2},... x_{i, m_i}}
- この時、g_n = XOR_k f(n, k)である。
- そして、g_S = XOR_{x in S} g(x)である。
アドホック †
- 基本的にはWLアルゴリズムやGrundy数を手作業で計算したり、実験コードを書く
- よくあるパターンとして、Nいっちゃダメ型がある
- この型では、状態をOとEに分けて、ある遷移でOからEを必ず押し付けられて、どんな遷移でもEからOになってしまう、という場合に使えるケース
- CADDi 2018 D - 「初期状態が E の場合、後手が先手の「真似」をすると先手は E に閉じ込められ、いずれ「全色 0個」に至り負けます。初期状態が O の場合は、先手は最初に奇数個の色のりんごだけ食べて後手に E を押し付け、それ以降は後手の真似をすることで勝てます。」
連立方程式・不等式の解を一例上げる †
和の等号 †
- n個のx_i + y_j = a_iなる条件を全て満たすようなx, yはあるか?
- =の条件はDFSで矛盾判定
- ちなみにx, y>=0の条件を加えても行ける(CODE FESTIVAL 2016 Qual A : D)
差の不等号 †
幾何 †
基本的な発想 †
- なんとなく連続っぽいので難しそうだが、実際にはイベントが発生するような点は有限
- このようなイベント点と、イベント点で何が起きているのかを把握する力が重要
計算のロバストネス †
- 誤差が非常に効いてくるケースが少ないので、なるべく計算誤差が少ないような演算方法が重要
点の進行方向 †
- ccwはロバストな進行方向の計算方法
- angle は三角関数の計算という不動小数の計算を必要とするが,ccw は係数環の演算だけで構成されているので,極めてロバスト
凸包構築 †
- 凸包は基本的にはO(n log n)
- 基本的にはAndrew's Monotone Chainを使うのがいい
三角形 †
多角形 †
- 最長辺が他の辺の総和以下になると多角形を構成不能に成る
Connectivity †
Incremental Connectivity = Union-Find Tree †
- 「同じ集合は同じ根を持つ木である。根は-要素数を持つことでsizeを持つ」である
- 工夫も実は簡単で、(1) uniteの時に木の浅い方にくっつける。 (2) Findの時に、通ってきた経路を全部根からの多分木にするである。
- 盤面問題をUnionFindで
ポテンシャル付きUF †
- 重み付きUFとも言われている(この名称やめて)
- 集合要素に環(分配・可換・逆元)であるときに、以下がO(A^-1(n))でできる。
| unite(u, v, diff(u, v)) | u-vが指定されて要素u, 要素vを同じグループとする。 | | find(u, v) | 要素u, vが同じ集合かを判定 | | diff(u, v) | diff(u, v)を計算 |
- 基本的に、辺(u, v, c)に演算をのせる時は、a_u+c=a_vとしたほうが色々無矛盾で良い
- 重み付きUF、頂点にRingが載っていて、任意の頂点対(u, v)の値の差を計算できると思うとすこしほっこりする
- 任意のアーベル群について、その要素をポテンシャルとして持つUFが作れるね。
Decremental Connectivity †
Dynamic Connectivity †
- 切れるUnion Find
- 追加クエリO(log n), 削除クエリO(log^2 n), 連結性判定O(log n / log log n)
- antaさんのライブラリがめっちゃ速い。
- 雑多情報
YES/NO †
- YES/NOで、1つYESがあった時に、それから操作してどれくらいの数があるかを探すとよい(乱択を狙える)
- 「もしYESならば…」という発想が必要
- もしYESならばAが真であるはずなので、Aとなるようなものを全探索しよう
- もし1つの解がYESならば、そこからちょっと変えた解もYESになる
乱択 †
- YES-NOを聞く全探索
- YESがあるならば、そこから何らかの操作をして別のYESを作れないか?と考える(ARC95E)
- n=1000でO(n^3)だから無理?
- しかし、YESがたったの1/n^3しか無いことはあるのだろうか?
- 例えばAOJ Symmetryでは、n^3個の中にn個くらいYESとなるケースがある。つまり、AmortizedでO(n^2)!
- なんとなく幾何と乱択は相性がいいような気がする
- http://www.slideshare.net/iwiwi/ss-13293754
- 恒等式をチェックする乱択
- Random Coloring
ヒープ †
- 二分ヒープがpriority_queue
- フィボナッチヒープが最速
Convex Hull Trick †
概要 †
- さばけるクエリ
- 直線f_i(x)=a_i*x+bをリストに追加する O(log n)
- max f_i(x) を計算する O(log n)
Increasing Convex Hull Trick †
- 直線の削除ができない!
- a_iが単調増加、xが単調減少の場合
Dynamic Convex Hull Trick †
- 更に、直線の削除が可能
- LiChao? segment tree
Mo's Algorithm †
- 点に全順序をつけるときに、iotaで生成したid数列をsortするというのが割とよいテクニックっぽい。Moの実装で全順序を与える時に使った
- Moの点群に全順序を与える時にiotaで作ったindex配列を作って、ラムダで位置i, jを固定してソートするやつ割と便利だった
貪欲 †
証明方法 †
- 順序を決める貪欲は、例えばAAAABBBBかな?と思ったら、BAとしたときにABよりも良くならないことを示せば良い
自由度 †
- n!の並べ方が許容されている場合、最適解への自由度は何個かある
- n!の順番はどうするか?実は、ある順番が極大スコアを得ないか?→隣接要素の交換により改善が示せる例
- 2^nの中から選ぶ方法はどうするか?→グループ分けの貪欲、もしくはDP
- n個のものをAかBに塗り分ける時、AAAAABBBBBBが最適ではないか?
隣接要素の交換により改善が示せる例 †
- 何を選ぶか?「最適な並べ方」を見つけるための貪欲
- AAAABBBBBとBBBBBAAAAAAはどちらがよいか?
- 数列の順番が固定ならば簡単に解けるため、最適解を与える順番は確定させたい!
- 交換以前の選びかたの可能性を最大化する。順序が決まっていればDPが実行できるので、順序だけ決めたかった。 Code Festival 2017 Final D
- 交換すると辞書順最小が得られる Code Festival 2017 チームリレーG
- Code Festival 2017 Final Dとほぼ同じ https://yukicoder.me/problems/no/054
- 順序の自由度を隣接2項間の関係で削ってからDP SRM 502 D1M
グループ分けの貪欲 †
- どういうsetを選ぶか?の貪欲
- a, bから被覆かつdisjointに取ってきて、何らかのスコアを最大化せよ!
- 基本的には、スコアの式において、aを選んでいた添字iをbに写した時に、どれくらいスコアが上昇するかの上昇幅でソートする
- 選ぶべき最小の個数とか言われたら、判別条件をf(a, b)>=0みたいな形に表しておいて、それをスコア関数にすればよい
- 数列a, bが与えられる。添字集合Sを取って、sum_S(a[i]) / (sum_S(a[i])+sum_{not S}(b[i]))>=P/100なるSのうち最小の大きさを求めよ(Code Festival 2017 チームリレーE)
- ++++++++++++---------が最適なので、その後-の順番と貪欲に取る JAG夏合宿Day 1 K - パンプキン
- 差を貪欲に取る CODE FESTIVAL 2015 予選A C問題 8月31日
まだ解いていない †
ビームサーチ †
証明の練習問題 †
- 貪欲に冠しては証明の訓練をするしか無い
- Topcoder SRM 697 D1E
- ARC 53C
- 上がって下がってする奴
- あの貪欲の構成は面白かった気がする
- AGC 03B
- AGC29 B
- 辺eをマッチングに使わないのならば、辺eを取ることでマッチング数を1あげることができる
- 次数>1を使うとすると、次数>1を使う他のマッチングe=(次数>1, v)があるが、マッチングとして使えなくなる朝展が次数>1, 次数=1, vの三点となってしまい、真に悪くなる
- 任意の頂点uについて、u-v とマッチするよりも良いマッチングの仕方があるとしたら、 a-u v-b みたいになってるはずで、対偶?を考えると、uがどれともマッチしない場合よりも何かとマッチしたほうが良い。
- u-v とマッチするよりも良いマッチングの仕方Xがあるとします。Xにおいてuもvも使わないなら、u-v使ったほうがよいです。Xにおいて u使わない & v-b よりも u-v, bフリー のほうが良いです。Xにおいて v使わない & a-u のときも同じです。
ハフマン符号 †
- 有名な貪欲アルゴリズム
- 2つ小さい方から取ってきて足したものをpriority queueに追加、を1個になるまで繰り返すと最適になる。
- 3つ取ってきて良い場合は、偶数奇数によって初めに何個取るべきかが異なるが、基本的には同じ
凸性 †
- 交換凸性チェックは、隣接したf(i, j)><f(j, i)をとくことで可能。これによって具体的な式も出てくるし、もし凸じゃなかったらダメだってこともわかる。
最大最小問題 †
- 最大最小問題は二分探索を考える
- [0, ans]が全て満たすような数え上げの最大化もできる (ARC 94E)
行列 †
行列の種類 †
0 1 0 0
0 0 1 0
0 0 0 1
a0 a1 a2 a3
- Toeplitz行列
- ある関数fが存在して(A[i][j] = f(i-j))と表せることを言う。
- Toeplitzであるだけでは乗算の元で閉じていない
- Blackbox linear algebraでは一般Toeplitzで動く。
- 上三角Toeplitz行列
- Toeplitx行列でかつ上三角行列のもの。
- 加算・乗算の元で閉じている。
- この行列はサイズnのベクトルによって表すことが出来る。
- 行列とベクトルの乗算は畳込みになっているのでO(n log n)
- Toeplitzであるだけでは乗算の元で閉じていない
- Blackbox linear algebraでは一般Toeplitzで動く。
- 巡回行列
- Toeplitz行列の特殊系
- 加算・乗算の元で閉じている。
- 加算はO(n)
- テプリッツ行列とベクトルの乗算はO(n log n log log n)
- 2つのテプリッツ行列の乗算はO(n^2)
- テプリッツ系 Ax=b は、レビンソン=ダービン・アルゴリズムでΘ(n^2)の時間で解ける。
a0 a1 a2
a1 a2 a0
a2 a0 a1
- あんたさんの巡回行列など行列累乗のライブラリがしたのほうにあるので、チュートリアルを作りたい
行列のクラスと計算量 †
| 名称 | 行列と行列の積 | 普通のk乗行列累乗 | k乗行列累乗(BLA) | | | 一般 | O(n^3) | O(n^3 log k) | O(n^3+M(n)log k) | | | 理論最速 | O(n^2.3) | | | 全く実用的ではないので、O(n^3)未満のものに期待してはいけない。理論最速に至っては、確率モデルに依存して実装不能 | | 巡回行列 | O(n^2) | O(n^2 log k) | O(n M(n) + M(n) log k) | | | (三角とは限らない)テプリッツ行列 | O(n^2) | O(n^2 log k) | O(n M(n) + M(n) log k) | | | K重対角行列 | O(n k^2) | O(n k^2 log k) | | | | S要素疎行列 | | | O(n^2 + n S + M(n) log k) | | | コンパニオン行列の累乗 | | | | |
- Blackbox linear algebraによる行列累乗
- O(n^2+n T(n)+M(n)log k)
- T(n): 行列とベクトルの掛け算
- M(n): 多項式乗算の時間計算量
- 単純なアルゴリズムではM(n)=O(n^2)だが、R=Z/mZの場合は余剰環上のFFTを用いることでM(n)=O(n (log n) log(log n))にできる。
- Blackbox linear algebraによる行列式
行列累乗 †
- 行列累乗そのものは任意の半環でできる
- 普通の行列累乗について、
- 行列累乗は行列を先に計算するとめっちゃ遅くなるので、行列xベクトルを計算しましょう。
- 構築ありの行列累乗だとメモ化できるので早い
- 参考 AOJ Three-way branch
行列式 †
- 普通には全体でO(n^3)
- 行列木定理と呼ばれる定理は、 グラフが与えられたとき、全域木の個数を行列式を用いて求められる
加群の行列演算 †
- 環R上の左加群なら、(+, *)じゃなくても行列演算が可能
- 零元と単位元が何かをものすごく気をつける必要あり。意識しないと死ぬ。
- 零元「足し算すると変わらない、かつ掛け算すると0になる」
- 単位元「掛け算すると変わらない」
- 普通の行列演算でいう0を零元、1を単位に書き換えないといけない。
コーディングイディオム †
漸化式 †
コンパニオン行列の累乗 †
- 二つの実装方法があり、後者のほうがメモリ効率が良いためかなり速い
- 行列の形に注目するもの
- 線形漸化式の線形性と、本質的に多項式の乗算除算であることを使う(つまりはこういうこと)
- その他説明
- コンパニオン行列の累乗(これが前者の方法で、これを実装すると遅いので注意)
- 古くは Krishnamurty [2] に発見され,その後 [1, 3, 4] によって再発見されている.
- ヘッセンベルク行列のべき乗への拡張は Datta and Datta [5]によって提案されている
- O(n^2 log k)
- コンパニオン行列のべき乗を計算する[Krishnamurthy,1960] On solving an algebraic equation using higher powers of an associated matrix and the Cayley-Hamilton theoremと同値..ヘッセンベルク行列への拡張が[Datta and Datta,1976]
最小多項式 †
- Aが密行列であっても、b_k = A^k b_0なるb_kの「1要素のみ」を取得するのはO(n^2 log k)
- これはそのまま、コンパニオン行列の累乗の一般化となっている。
- 高速きたまさ法でO(n log n log k)にもなる。
- ケイリーハミルトン
- 行列列{A^i}を零化する多項式はたかだか次元n
- ベクトル列{A^i c}や{b^t A^i}も零化する多項式はたかだか次元n
- 数列 {b^t A^i c}も零化する多項式はたかだか次元n
- つまり、(0, 0, 0, ..., 1) A^k bなど、一要素を取り出しただけならば、この最小多項式はn以下
- 2*n個列挙すれば、その最小多項式を計算することが可能(Berlekamp-Massey algorithm)
- 最小多項式が計算できるということは、きたまさ法に帰着できたということに他ならない。
- したがって、O(n^2 log k)で計算ができた。
- ちなみに、Aが疎行列であっても計算量は落ちない
- 右上のみ1の2次行列Aとb_0=(100,1)に対して、b_0(1),b_1(1),…は100,1,0,0,…となりますが、これが1項間線形漸化式で表せない
- 最小多項式は[0, 0, 1]になるので
逆行列 †
- 解き方
- 掃き出し法 O(n^3)
- Black Box Linear Algebra O(n T(n))
- 最小多項式計算→クリノフ列 O(n^3)
- b, Ab, A^2 b...と、最小多項式次元数n個計算して、後で足す。
- 実は掃き出し法と同じ計算量なんだね
#include <Eigen/Dense>
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
using namespace Eigen;
auto I = Matrix2d::Identity();
int main(void) {
Matrix2d A;
A << 3, -2, 1, 0;
// f(A) = A^2 - 3A + 2I = 0
vector<double> phi = {1, -3, 2};
Vector2d b;
b << 2, 4;
cout << A << endl;
cout << A.inverse() * b << endl;
cout << -1.0 / phi[2] * (phi[0] * A + phi[1] * I) * b << endl;
return 0;
}
全方位木DP †
- 基本的なアイディアは、DFSを2回行って、2回目で親から来た辺1本だけを例外扱いすれば良い、ということ。
- どこか根からDFSすると、親の情報以外は確定するんだけど、親の情報だけはわからなくて悲しいので、一度親に遷移して必要な情報を求めて戻ってくると、ある頂点iの周囲全ての情報が分かることになる。
- 実装上は、一回戻って、とかやってると非効率なので、vからnext_vに行く時に自分の情報を渡してしまうとよい。
- 木はu, vで次の頂点を表すとバグる(u, vが似ているので)
- 全方位木DPでは、親から来る情報dparは、data[i]と同等の情報を復元しなければならない!!ここに悩むポイントはない!!以下のように、悩まずに求めるべきものは確定している
- 実装上は番兵をおくのがセオリー(親が根の場合に特別扱いする必要があるので)
- 例題
- s8pc 4: Data[i] = 頂点iから見て頂点0がある辺を削除した時の、頂点iから見た期待値。Dpar = 「頂点pから見て頂点iがある辺を削除した時の、頂点pから見た期待値」。
数え上げ †
DP †
- グルーピング系の数え上げは結構freqでやるのが良さそう
- DPで同じ状態にまとめようと思った時に、分割するみたいな発想(バカの一つ覚えのようにi個見て…とかばかりしない。)
- 逆順のDPの場合、DP[i+1][j]からの遷移を考えたほうが楽
ちょうどXとなるものの数え上げ †
- ちょうどXは厳しいので、「X以上の関数定義」と「X以下の関数定義」などを構築しておくとよい
- ( # f(x)=N ) = # f(x)≦N - # f(x)≦N-1
カタラン数 †
無向グラフの頂点iから頂点jにちょうどk歩で行く場合の数 †
- 参考
- 「無向グラフの頂点iから頂点jにちょうどk歩で行く場合の数」=「隣接行列Aとする。A^kのi, j成分」である。
- 閉路を考えるなら、i==jとすればよい
- 注意点
- 交差しているものも数え上げる!
- i=A, j=B, k=4としたとき、A->B->A->B->A->Bとかも数える。
無向グラフのk歩で戻ってくる閉路の個数 †
- 無向グラフのk歩で戻ってくる閉路の個数
- 開始頂点は指定できないので注意!
- k=3からk=12くらいまでは公式がある。
- 公式は非常に複雑なので、ここを見るか、ライブラリをそのまま使う。
無向グラフの全域木の数え上げ †
- 「無向グラフの全域木の数」=「ラプラシアン行列のn-1次部分行列の行列式」
- ラプラシアン行列とは、n行n列行列で、その (i,j) 成分が
- i=jのとき、頂点iの次数(=頂点iから出ている辺の数)
- i≠jのとき、隣接行列の(i,j) 成分の−1倍
- 行列木定理 (Matrix-Tree Theorem)と呼ばれているもの。
二部マッチングの数え上げの偶奇 †
- 隣接行列の行列式で計算できる。
- 二部マッチングの数え上げそのものはNP完全
元の隣接行列
011
110
011
数え上げるべき組み合わせ
001
100
010
010
100
001
転倒数の数え上げ †
- 問題そのものは「クロッシング問題」と呼ばれる。
- 要するにバブルソートの交換回数。転倒数は反転数とも呼ばれる。
- 愚直にはO(n^2), 普通にはO(n log n), 世界最速はO(n sqrt(log n))
- 解法
オイラー閉路の数え上げ †
- BEST theorem
- オイラー路はグラフの全辺を使うパス
- オイラー閉路は、閉路であるオイラー路。
格子点に頂点を持つ三角形の内部の点数 †
二分探索による数え上げ(の最大化) †
- 大抵、数を決めると貪欲が効いてうまくいく、みたいな構造になっている
- ARC 91D
- ARC 94D
- 数を固定すると、数列のelement-wise積の最大値がX以下か?という問題に落ちる
式変形のデバッグ †
- 式変形でミスしたことがわかったら、式に出てくる変数に小さめの数を代入して、式変形を一行ずつたどることで式変形をデバッグできる
包除原理 †
- 「すべてのトッピングも2種類以上乗っている→あるトッピングが1種類以下」を引き続ける→これは包除原理、みたくなる
- 包除原理は、「異なる玉8個を、異なる箱3つ x_iに入れる方法の中で、全ての箱に1個以上入っているような場合の数を求めよ」が簡単な例題である。
答え
= |全事象| - |x_1に1個未満入れる方法の集合 ∪ x_2に1個未満入っている集合 ∪ x_3に1個未満入っている集合|
= 3^8 - (3C1 [x_1に1個未満入れる方法の集合] - 3C2 [x_1に1個未満いれてx_2に1個未満入れる方法] + 3C3 [x_1に1個未満いれてx_2に1個未満いれてx_3に1個未満入れる方法])
= 3^8 - (3*2^8 - 3*1 + 1*0)
- 多次元の包除原理
- 「条件A_iがn個与えられて、k個以上条件を満たす〜を数え上げよ」という式を考える。k=1では、ちょうど1個満たす時の和がだいたい答えかなー、でもそれだとちょうど2個満たす時の和が重複しているから消そうなー、でもそれだとちょうど3個満たす時の和を消しすぎたなー…とやっていくのが包除原理。(ベン図を考えると、k=0の時は普通に全事象で、それ以外の時に意味があることがわかる)
- 包除原理は大抵非常に数学ゲーになる
- Codeforces 493 D2E
確率 †
- 総和の総和
- Code Festival 2018 Relay E
- 数え上げを期待値の計算だと思うことで、その嘘っぽさを期待値の線形性の嘘っぽさに押し付けることができる
- 期待値の線型性 E[X+Y]=E[X]+E[Y] は、XとYとが独立でなくても使えるのが強い!!
重複して数えていないことの確認 †
- 数え上げはdpなのでdagと仮定して,
- 状態iから状態jに配るときに, i → k → j と配られる k が存在しないか, 存在しても i → j と i → k → j は異なることを証明することで納得しています
- 数え上げでは、事象をdisjointな集合に分けてそれぞれ数えて足し上げるということをよくやります
一般化川渡り問題 †
- ボートサイズ2で多項式時間
- ボートサイズ3でもコネクティビティだけなら多項式時間だったり
Blackbox linear algebra †
参考 †
原理 †
概要 †
- 行列累乗
- 普通O(n^3 log k)で、テプリッツ行列・巡回行列・コンパニオン行列などでO(n^2 log k)だった。
- めちゃくちゃ大雑把にいうと、これのlog kを分離してO(n^3 + log k)やO(n^2 + log k)にする手法
- 以下の時、「線形漸化的」であるという。(antaさんの造語?N階線形漸化式を満たすという表現)
- これはまさに、無限列が実は初期値+線形多項式で生成できる、という意味!
Vを体F上ベクトル空間として、V上無限列{a_i}がある。
ある多項式cが存在して、
c(x) = c_0 * x^0 + c_1 * x^1 + ... + c_n * x^n
全てのiについて、
c_0 * a_i +
c_1 * a_i+1 +
c_2 * a_i+2 +
...
c_n * a_i+n = 0
- 線形漸化的な無限列は、多項式cの空でない集合を持つ。
- cをうまく取ることで、最小次数を有しかつ最大次係数が1となるような多項式を唯一に選べる。これを最小多項式と名付ける。
- 行列Aに対して、無限列{A^i}は線形漸化的である。
証明: ケイリーハミルトンの定理により、c(A)=0。
任意のiについて、
c_0 * A^i +
c_1 * A^i+1 +
c_2 * A^i+2 +
...
c_n * A^i+n =
A^i * (
c_0 * A^0 +
c_1 * A^1 +
c_2 * A^2 +
...
c_n * A^n) =
A^i * c(A) =
0
- 最小多項式は、「最小多項式の次数の上限n」「列の先頭2n要素」の2つだけで構成可能
- 体上の最小多項式は、Berlekamp–Massey algorithmで計算できる。資料
- 体上のベクトル{b_i}の最小多項式は、ランダムベクトルuを取ってきて、{u^t b_i}の最小多項式と高確率で一致する。
- 体上の行列{A_i}の最小多項式は、ランダムベクトルuを取ってきて、{A^i u}の最小多項式と高確率で一致する。
- 最小多項式が既知ならば、線形漸化式の第j項はO(k^2 log j)で計算可能。
b_i = a_i
b_i+k =
c_0*+b_i+0 +
c_1*b_i+1 +
...
c_k-1*b_i+k-1
f = x^k - c_0 x^0 - c_1 x^1 - ... - c_k-1 x^k-1
x^j mod f = d_0 * x^0 + d_1 * x^1 ... d_k-1 * x^k-1
x^2n mod f = [xの2k-2次多項式] mod f = [xのk-1次多項式]
O(k^2) ①
①はx^i (i <= 2k-2)を前計算O(k^2)することで、O(k^2)で計算可能。
最後の合成ではlog j個の掛け算を行うので、全体でO(k^2 log j)
多項式 †
畳み込み †
- FFTとかNTTを使うとO(n log n)で計算できる
公式 †
- 総和の分解
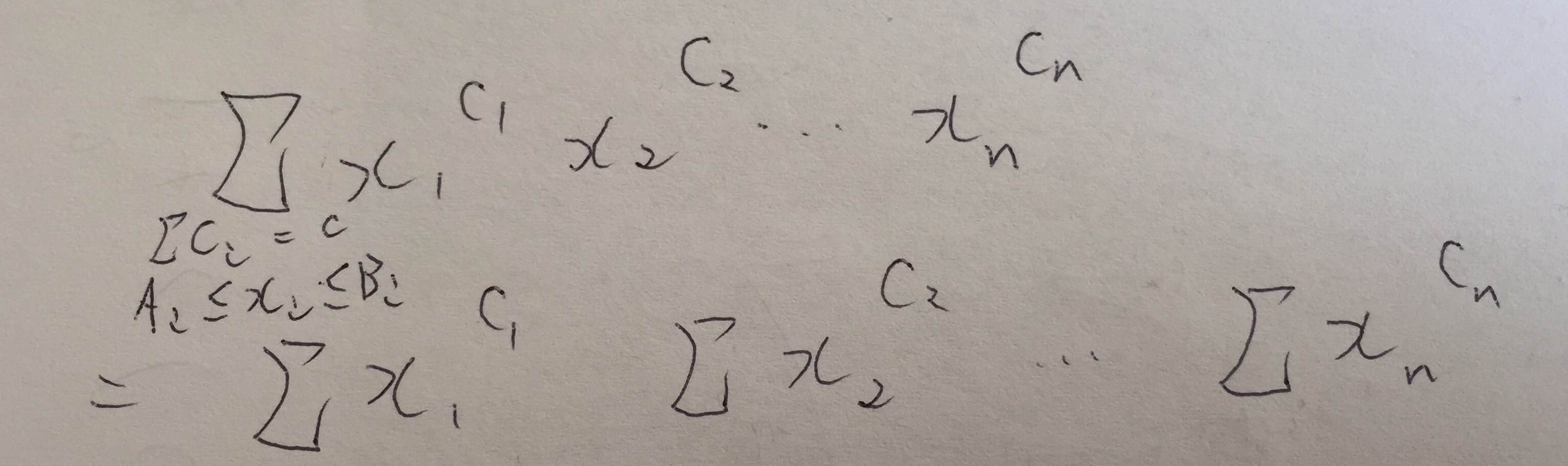 - ARC 59C
- くくりだしの漸化式
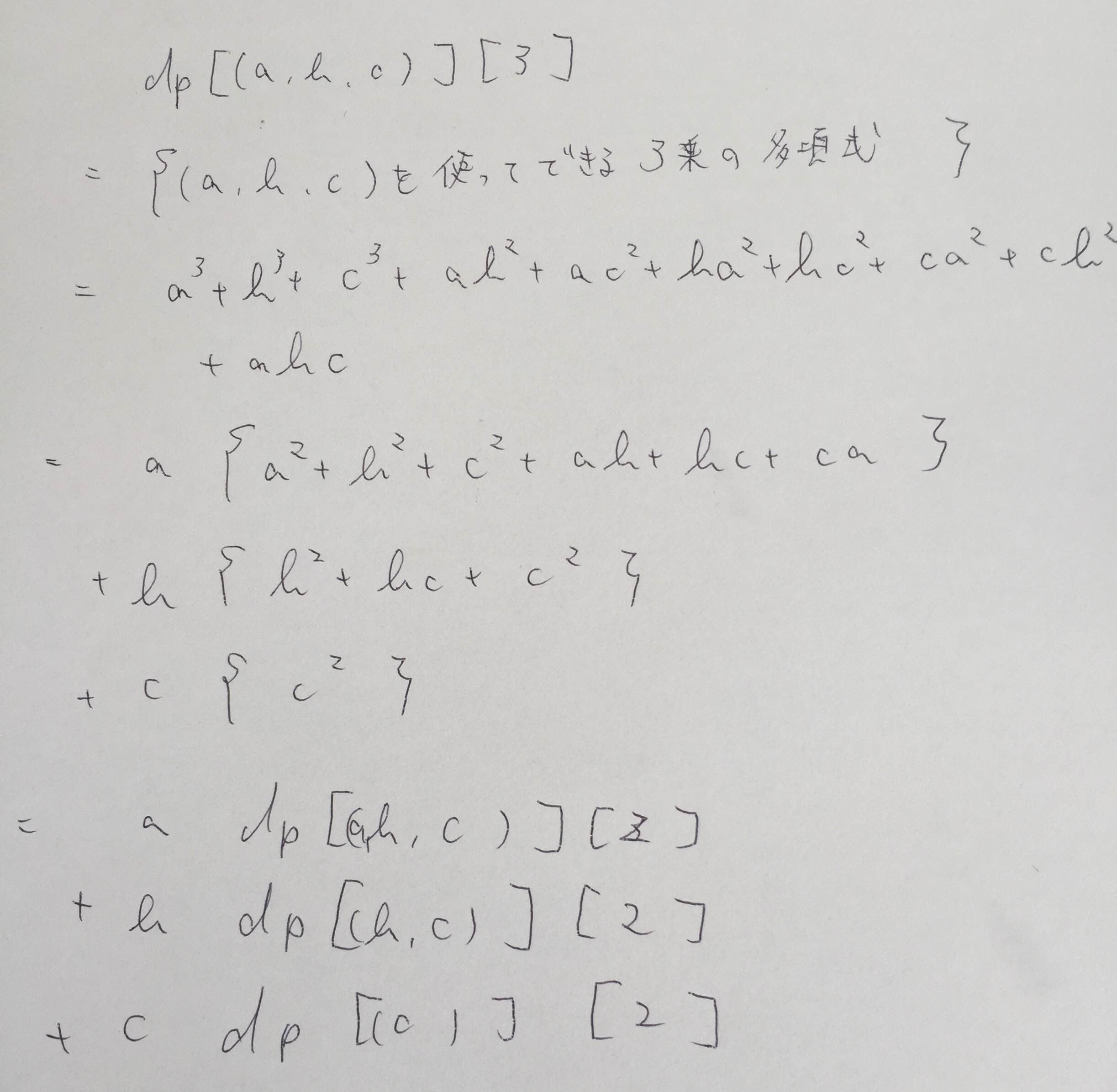 - ARC 59C
ラグランジュ補完 †
- N次式で(N+1)個の値がわかっているので、ラグランジュ補間で完全に式を求めることができる。
母関数 †
- 漸化式と母関数 [#ya65cdad]
- 講義資料
- 漸化式→母関数
- 母関数→一般項は非常に簡単
- 母関数fが有利関数ならば、漸化式は線形漸化的
- f=g/hとすると、1+deg h次の線形漸化式となる。
- 母関数を直接求める [#pa2f69f3]
- 母関数が先に簡単に求まるケース
- 「正整数の列aが与えられるとき、aの重複なし部分和でちょうどbになるものは何通りあるか?」=「f=∏(1+X^{a_i})f=∏(1+X^{a_i})とするとき、fのb次の係数を求めよ」
- 「正整数の列aが与えられるとき、aの重複あり部分和でちょうどbになるものは何通りあるか?」=「f=∏Σ(1+X^{j*a_i})f=∏(1-X^{a_i})^{-1}とするとき、fのb次の係数を求めよ」
結合性 †
expand(subst(subst(a3*x+b3, x, a2*x+b2), x, a1*x+b1));
expand(subst(a3*x+b3, x, subst(a2*x+b2, x, a1*x+b1)));
- 3次
expand(subst(subst(a3*x^2+b3*x+c3, x, a2*x^2+b2*x+c2), x, a1*x^2+b1*x+c1));
expand(subst(a3*x^2+b3*x+c3, x, subst(a2*x^2+b2*x+c2, x, a1*x^2+b1*x+c1)));
高次連立漸化式の係数変更クエリ †
- まず、漸化式を愚直に代入すると、各漸化式毎に出てくる項は有限であることがわかる。
- 従って、各漸化式ごとに、1つ前の係数から次の係数を計算する行列を計算することができる。
- これを対角に連結(してもしなくてもいい)すると、行列連鎖積*初期値になるので、Segment Treeで計算できる
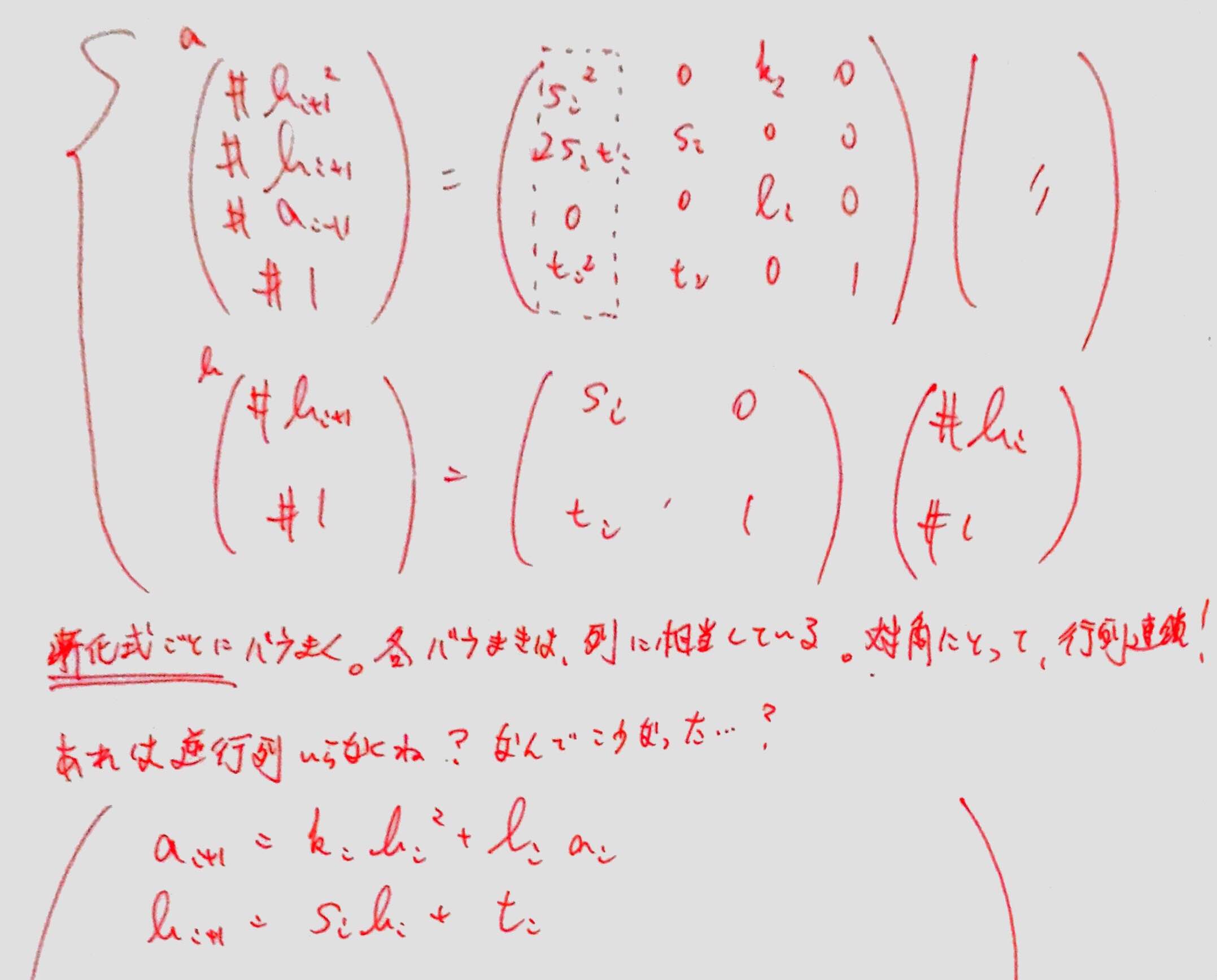
点群処理 †
2つのsetを同時更新 †
- 範囲のどれかが0であれば、2つのsetを同時更新するだけでkd-tree相当の処理がO(log n)、しかもnot amotizedで処理可能
- set<int, int> fs, sf; // first-second, second-first
- CF 366 D2C
kd-tree †
- 平衡Dynamic kd-tree
- spaghetti codeにあるやつ
- 二次元閉区間の点を追加、点を削除がO(log n + k), k=ヒット数、amortizedで処理可能。
- 点に情報を乗せることもできるはず
- スケープゴート的に平衡処理する
- CF 366 D2C
応用:2D Euler Tour †
- iwiwi先生の木のクエリ完全制覇
- 1D Euler Tourだと群的データしか載せられなかったのが、これだとモノイドも載せられるっぽい
ラグランジュ補完 †
Zeilberger's Algorithm †
盤面 †
上書き †
DP †
盤面の一致判定 †
マトロイド †
- よくわかってないし必要かもよくわからない。
- http://d.hatena.ne.jp/drken1215/20121212/1355280288
- ある集合がマトロイド=ザイズが同じ一番大きな集合を何個か持ってきたものをマトロイドとする
- マトロイドの基=極大独立集合
- マトロイドの集合から任意個数の要素を削ったものをマトロイドに加える
- このように出来たものがマトロイド
- マトロイドの要素は「独立な」集合と呼ばれる。
- 単位時間ジョブスケジューリング問題(http://topcoder.g.hatena.ne.jp/spaghetti_source/20121103/1351911603参照)
- ベクトルマトロイドに用いる問題(SRM 526.5 DIV1 Hard)
- 行列Aが与えられたとき、Aの列ベクトルをa_1, a_2, …, a_nとすると、M = {a_1, a_2, …, a_n}、I = (Mの部分集合のうち、一次独立なモノの集合)とすると、(M, I)はマトロイドとなります。これはベクトルマトロイドと呼ばれます。
- グラフの枝集合に対して森はマトロイド。最大独立集合は全域森
- 2つの基に対して、かぶっていないものを交換しても両方ともマトロイド。これをマトロイドの交換公理と呼ぶ。基と基でこれをやると、同じように交換後も基である。これは凄くて、凸っぽい。
- マトロイド(M, B)に対し、ある基Sが与えられたとすると、以下の2つは同値である。「Sが最大重みの基」「Sの近傍となる基S^’で、Sよりも重みが大きい基は存在しない」これはまさにGreedy!
Gray Code †
- ハミング距離が常に1の表現
- 使い道
- アブソルートロータリーエンコーダで隣り合った角度のハミング距離がでかいとこまる
- 遺伝アルゴリズムで使うと性能が上がる
定数倍高速化 †
ループ内部の処理を前処理に回す †
- DP内部での処理を軽くするタイプの定数倍高速化は結構効く(40倍くらい早くなった)
データ構造の低次化 †
- map->unordered_map->vector->配列
ullのmodは早い †
unsigned long longにして mod 演算を高速化したり,必要になるまでO(N)の更新を後回しにする,とかやったら通りました(更新,取得,更新,取得,...の順でクエリが来るN=10^5,Q=2*10^4のケースありますか?)
vectorのreserve †
ループアンローリング †
- ループアンローリングで20%くらいの高速化できることがある。
- キャッシュが乗るらしい。よくわからない。
emplace_back †
- moveが呼ばれるので少し早い
- たとえば以下の2つはほぼ同じだが、メモリ確保回数が減る
vector<vector<int>> vvi;
vvi.push_back(vector<int>(10));
vvi.emplace_back(10);
bit並列 †
- これは「細々として」ないかも
- bitの状態をまとめて持つことによるDPの高速化。64bitだと64倍高速化になることも!
- intが32bitなのに対して欲しいものが8bitとかの時にまとめて計算する並列化手法。文字列でよく使われてる
- 例題
SSE †
- SSE?
- SSE具体的には、mask使うとifを簡単に表現できたりするけど、コンパイラもそこまではやってくれないとか
キャッシュ †
- やるべきこと
- 配列の走査順を適切にする
- DPでは、多くループが回るものを、ループの内側にすると、早くなる。
- メモリ確保時にはできるだけ一括して確保する
- 関数使わないとキャッシュが効きやすくなることは基本的にない
- 関数をなくして早くなるのはスタックを積むコストを無くせるからですが、現代ではinline関数で書けば十分なケースが大半だと思います。
枝刈り †
modを使わない †
intよりuintが早い †
- おもに%, /が速いので、ギリギリなら/, %を使う良い
メモリを使い回すDPは速い †
Dancing Links †
- 疎行列の「列を削除する」「行を削除する」みたいな操作が高速に行える。
- Knuth’s algorithm X
- Exact Covering({1, 4}, {3}, {1, 2, 5}, {2, 5}で、{1, 2, 3, 4, 5}をきっちり作れるか?)という問題が速めに解ける(この問題自体はNP完全)。この問題は疎なのでdancing linksが有効。
- また、Exact Hitting(集合は、中に入っている数字を一つ選ぶことで、殺すことができる。全ての集合をちょうど1回ずつ殺せるか?)は、Exact Coveringと同値。Exact Hittingはいい感じの解釈ができて、状態を「ある場所xにiを割り当てる」場合にx_1からx_iを作っておく。その後、制約条件を「a_1, ... , a_kのうち、ちょうど1つしか満たされない」という形で表すと、Exact Hittingに帰着する。
- また、SudokuはExact Coveringなので、これでいい感じに解ける。
埋め込み †
- 漸化式の途中計算を0, 10000, 100000などと埋め込むことで、高速化する方法。
- 式そのものを埋め込むことも
Range Tree †
- 特に、指定された区間や点にオーバーラップする全ての区間を探すという問題を効率的に解くことができる。
- 例えば、表示されている地図内に見えている全ての道路を求めるとか、3次元のシーンで見えている全てのオブジェクトを求めるといった用途に使われる。
「データ構造をマージする一般的なテク」 †
- 挿入が定義されたデータ構造がn個ある。この時「片方Aのデータを全てもう片方Bに挿入し、Aをclearする」というマージ操作において、必ず|A|<=|B|とする。すると挿入操作をO(T(n))として
- 最悪計算量O(n log n T(n))
- ならし計算量O(n T(n))
- なお、集合サイズの制約がないと、最悪O(n^2 T(n))となる。
- 「挿入が定義されたデータ構造」とは?
- vector
- set
- priority_queue(併合をサポートするLeftist HeapやSkew Heapで併合ならしO(log n)なので、そっちを使うべき)
- Quick-Findはvectorでこれを行ったUnion-Findもどき
整数計画法 †
- 大概のアルゴリズムは整数計画に落ちる
- 綺麗な形なのでなんとなく楽しいが、実際に解くのはNP困難の上、IPソルバは非常に長いので現実的には使えない(と思っている)
- 整数計画に落としたあとに、多項式時間で解くためのコツをまとめる
変数定義 †
証明でよくある手法 †
- S=Σxと置く。
- Sから1つかけているなら、S-x_iときちんと変形
- T>Sなる超大きな定数を前提する(あとでそのようなTが存在することを示す必要あり)
=存在性証明の顔をして一例あげてしまう
存在性証明の顔をして一例あげてしまう †
- 存在性証明は、順逆の証明をするのだが、まるで二回順方向に証明しているように示す
- まず必要条件を示す
- つぎに解を具体的に提示(むつかしい。元の拘束条件から求める)
- その解を拘束条件に代入して、必要条件と同値を示す

数値計算 †
n次収束とは †
pow, logを減らす †
- 求根では、全体にlog, expをかけても結果は変わらない(これらは遅い)
Householder's methods †
- 求根アルゴリズム
- 1次はNewton法に一致(C1を前提, 2次収束)
- 2次はHalley法に一致(C2を前提, 3次収束)
- Newton法
- Halley法
- x <- x - (2 f(x) f'(x)) / (2 f'(x)^2 - f(x) f''(x))
- 直感的には、交点・接線・凸性を保存した二次関数の極値に飛ぶ。
ランベルトのW †
- y = x log xの逆関数。
- Halley法で超高速収束(3次収束)
- Halley法を計算すると、\( x_{n+1}=x_n-\frac{xe^x-z}{e^x(x+1)-\frac{1}{2}(xe^x-z)\frac{x+2}{x+1}} \)
- 2回3000、3回48058、4回31150、5回1117でしたので、平均3.89回イテレーションで4e-16の誤差
数学 †
遅延伝播 †
謎木 †
- 謎木によるordered setの実装。lglg n
- van Emde Boas木として知られている構造はMビットユニバースに対する上位ビットサイズを H(M) = M/2 に選んだデータ構造
- ところが,vEB木はその計算量インパクトと比べてほとんど実用はされていません.
- これはvEBの計算量ゲイン:log(U) vs loglog(U) が効いてくるには十分大きなユニバースでないといけないのに対し,そのような大きなデータの処理では,データアクセスのオーバーヘッド(ファイルの読み出し等)が支配的になってしまい,もっと単純でデータ配置に即したB木などの構造のほうがトータルで早くなるから
ハッシュ †
- \( n \)bitのハッシュは、期待値\( 2^{n/2} \)個の相異データを突っ込むとぶつかる
- 32bitハッシュで65536個
- 64bitハッシュで4e9個
- 誕生日365日は、\( \displaystyle \sqrt(365)=18 \)人くらいもってくるとぶつかる!(この意外性、思い込みを突いた衝突攻撃を誕生日攻撃と言う。)
- md5sumのヒット率
- ロリハのヒット率を調べたい
- md5sumの結論は、要するに、ハッシュの質が良ければ64bitハッシュで十分
- ハッシュのデータ型は、size_tではなくて、uint64_tなどbit数が明示されたものを使いましょう
- 32bitのハッシュは65536個でぶつかるので死にます。
簡潔データ構造 †
細々とした実装テクニック †
- a*nのオーバーフローのチェック
- if(a*n/n==a) cout << “no overflow” << endl; // オーバーフローしてたら
- if(a * 1. * n < (double)LLONG_MAX/*2e18とか雑でも可*/) cout << “no overflow” << endl; // 精度落として計算してみる
- find_ifとall_ofを使うべき。
- find_ifのexistsとしての使い方
auto it = find_if(all(memo), [&](P x){return x == 1;});
if (it != memo.end())
hoge();
else
huga(*it);
- グラフDFSのメモ化の時に、遷移前にusedを見るとちょっと早い(2倍程度)。いってみてからusedを見ると、遅い。
- swapやるべきときは、ループのはじめにやるrep(_, 2) { swap(a, b); みたいなかんじで。なぜかというと、最後にすると途中でcontinueすることがあるのでバグる
- tieは辞書順なのでこんな感じにすると辞書順比較関数を作ることができる。
std::tie(n, s, d) < std::tie(rhs.n, rhs.s, rhs.d);
- 5000だとllのO(n^2)空間計算量だと、MLEこわいのでint32_tなどきちんと明記
- 乱択で順番を変えたい場合はrandom_shuffleを使うと良い
- randはクソ(環境依存、質が悪い)ので、xorrandを使いましょう。
- 左右の両側から試さなければならないばあい、対称ならreverseを最後に入れてrep(_, 2)で囲む
- 配列のrotation操作
- 円環数列は実は、a+aを考えてやると作れてしまう。
座圧 †
- 座圧でソートした後の数列は、「(v, id)がi番目に小さい」という意味がある。
- 「i番目に大きい位置」「i番目に大きい値」をO(1)でクエリできるようになると思っておけば良い
括弧列 †
- 正しいカッコ列は、(が必要な数と)が必要な数を管理すると良い
- 正しいカッコ列にするために必要な(と)の数について(SRM688D1M kmjpさんのdodo、「下がりすぎなら(だとみなしとく、つまり必要」)
- 床突き抜けたらダメなので(に強制的にする
- 今後全部)じゃないといけないので強制的に)にする
構築 †
- ジャッジの作り方を考える
- 同じ条件で、取り除いたり足したりすることができるかなどを考える(ARC91E)
- 「最適解を1つ持ってくると」からはじめて、どういう操作が改善するかを絶対に考えること!!!
- 構築の時に、演繹的に「どんな構造が欲しいか?」と考えるのも大切だと思うんだけど、逆に「こういう制約を加えた時に構築可能か?」みたいなDPの状態ガチャみたいなことが必要なのだろうとは思う(そこまで到達していなかったけど)
YES/NO †
- 乱択
- 乱択はギリギリっぽくてもわりといける(乱択マジック)がある
考察 †
基本 †
- まとめ
- 逆から見る
- グラフ
- 同一視
- 最小の操作回数
- 制約をきちんとグラフ構造で記述する
- gcdで同一視、3乗で同一視、衝突し得るもので同一視
- とりあえずこういうものがある、と決め打ちして考察
- ソートする
- 辺に着目すること
- 値でソートする
- いろんなものに着目する。点、辺、面、グリッドなど
- 自明な条件の列挙、「プレイヤー1がこれ以上改善したいならば…」
- フローか?DPか?二分探索か?などなど、とにかくいろいろ考える
- わからなかったら問題制約を減らす
- 貪欲的に考える(もしこの状態からより良くしようと思ったら…)
- 数直線で考える
- 「1時間考えても解けない!」みたいなパターンって、全然違うところで思考が無限ループに陥ってる、みたいな感じ
- 「30分解けなかったら思考をBFS的にしていったんリセットする」みたいな感じのことをする
- 貪欲的な思考(大概の天才問題が解けないのはこれのせい)
- Mujin Programming Challenge 2017 - A - Robot Racing
- AGC 18B
- 数直線で考察
- SRM688D1M(区間を数直線みなして、各場所から始まるvvllで管理)
- 同一視
- AGC003D(3乗で同一視)
- Codeforces 431 D2D(ぶつかり得るもので同一視、グループ化)
- SRM605D1E(プラスマイナスがふらふらするのはめんどいのでABSをとっても同値)
DP †
- まとめ
- ちゃんと紙の上に式を書く
- 表を書いて、込み入った矢印をシンプルにする
- 配るのともらうの、両方ともきちんと考える。もらうほうがデータ構造的との相性が良いケースが多い。
- 制限付きの状態をきちんと考える
- DP内部に入り込んだ謎の情報も、漸化式表現にすることでDPに組み込める可能性
- 制限付きDP
- Codeforces 416 D2C(「座標iの右端にかぶる区間の左端がiを全て上回るような…」とかいう意味不明な状態を含める)
- SRM 653D1E 複数制限があるけど、初めにあたった制限のみを展開すると、再帰的に網羅できる。
XOR †
- まとめ
- 桁ごと見ていくしか無い!!
- Trieで上の桁から決めていく
- XORは偶数奇数と見れる(mod 2の和と同じなので)
- GF(2)の加算としてのXOR(XORは、余剰体Z/2Zの加算演算である)
- Trieを使うことでXORをO(log n)で最大化することができる。
- 累積和するといいことがある [#u0c36487]
- XOR範囲和が0となるような範囲の数え上げ SRM 565
- g_i+(g_i-1)は高々log n個
- Grundy数なんだけど操作g_i->(g_i-1)を表現するのつらすぎるのでg_i->g_i+g_i+(g_i-1)とすると、g_i+(g_i-1)が高々30通りに
- xorを組み合わせて何かを作ろう系
- kビットのベクトルを組み合わせて目的のベクトルを作る的な発想になると連立方程式に落ちて掃き出せば大体解ける
- 1 bitのxorはmod 2の剰余体なので、整数はF_2^d (dは2進数桁数)のベクトルであると言える。行列に関する吐き出し法や逆行列の考え方を使うことができてしまう
GCD †
- まとめ
- 数直線で考えて、小区間に分解(O(log n)になる)
- 包除原理
- gcd系で数字が小さい場合は数直線を考える
- Codeforces 432 D2D
- 理由:gcdで合わせるのは小区間についてのクエリが効率的に求まるならばO(AMAX log AMAX)が可能(調和級数で、gが増えていくと小区間の長さはn/gなので)
- 包除原理
- CF 428D
- Atcoder ABC ??D LCM Rush
- 上から見ていくと、素因数の集合みたいな変なことをしなくてもO(n log n)で行ける
回文 †
- まとめ
- 長さの小さい順にDPする(長さ0, 1が自明な回文となる)
- メモリが足りなそうならばmanacher, SA-ISで高速化・省メモリ化
重複を除いて・種類の数え上げ †
素数 †
- まとめ
- 因数分解すべき数nが大きい場合、n^1/3まで列挙。これで残った素因数はp, pq, p^2, 1に限定される。
ペアの数え上げ †
- まとめ
- count_{l, r} f(l)<=f(r)に頑張って落とす
Subsetの数え上げ †
- Subset sum:値域に着目すると、リスト+=シフトリストをひたすら繰り返すことによって可能
- サブセット和を値域で分類して数え上げるテクニック(スライド和を使う)
- リストのスライド和のコーディングイディオム(逆から舐める)
- list += list>>kは逆順にループを回す
文字列 †
- Aho空間
- Leetcode 639(Aho空間でのDPは重複ありなしをきちんと考えないと、失敗辺をどうするかが混乱する。重複なしAhoのDPの遷移は、「そのままやる」or「失敗してからやる」となる)
グラフ †
- まとめ
- パス→木はとりあえず根付き木にして、パスは(lca-a)+(lca-b)-2(r-lca)とする
- 部分木→オイラーツアー
- 重心は子がn/2以下で嬉しい。LCAとかにしたい。
構築 †
- 数字
- グラフ
- ウニ、line、二部グラフ、木、クリーク、補グラフ
- ゲジゲジグラフ
- Functional Graph
典型問題 †
- \( 数列c_i \)と\( x \)が与えられる。この時、\( \displaystyle \Sigma a_i c_i = x \)なる\( a_i \)のうち、\( \displaystyle \Sigma a_i \)が最小のものを求めよ。
- 一般にはNP困難だが、\( \forall i\ a_{i+1} = 0 (mod a_i) \)の時には、少なくとも貪欲で十分。
- 証明「ある桁に\( c_i \)以上の数字があるならば、最小手数ではない。(\( c_i \)減らして次の桁に移すと\( c_i-1 \)減らせるので)」\( \Leftrightarrow \)「最小手数ならば、全部の桁が\( c_i \)未満」
- 「最小手数ならば、全部の桁がb未満」の証明だけでは、他の手順で評価値を良くできる可能性があるのでは?→他の手段とは→b^次数差の行き来のみで全係数の操作を網羅するから最小性が言える
- Nth-number
- BITの二分探索で探すのが常套手段
- 追加削除は値域方向に展開して、有効無効のフラグを管理するのが常套手段
- 数字のやりとりは右から左へと数字を流していって、abs(流れた石の量)によって計算できる
- ソートされた一次元の点x_iがあり、その中で全点との距離が最小な点はx_{[n/2]_l}
- \( x_i (i = 0...n) \)に対して、\( \Sigma abs(x_i - l) \)が最小となる数lを求めよ
- 中央値を求めるだけでいい(平均値ではない!)
- 理由:左右見て数が多い方があればそっちに移動したほうがいいので。
- 1,2,5,8なら[2,5]の全数字が解、1,2,8なら2だけが解。
- \( ax+y=c (x \in [0, X], y \in [0, Y]) \)なるx, yは存在するか?するならば一つ挙げよ
- xを[0, min(X, c/a)]の範囲で二分探索(c-ax<=YならOK)。
- minを取ると、yが0以上という条件が必ず満たされるようになるので、特性関数が単調になる
- 数列aが与えられる。a[0:i]の上位k個の総和を全列挙せよ。
同一性カウント †
- 普通に考えてメモリ上に並べてソートして、隣接前後を比較するだけでいい
- Codeforces 391 D2C
- Vectorのcounter
- この方法だと、vectorのようなものであっても普通にカウントできる。
- mapにvectorをつっこんでもいいけど、まあメモリと比較が重そうなので。
構成問題 †
- 条件がきついから綺麗な構成があるはずだ/こんな条件適当にやれば満たせるやろ の区別は割と楽につくはずで、前者だったら適当な仮定のもとで理詰めするとか制約から感じるとかcheckerの作り方を考えてみるとかいろいろあります
- 2-SAT(2-SATの解は選べないため)
- 乱択(乱択の解は選べないため)
- TopCoder? 2018 TCO R2A Hard
- イミフ構成はわりかしこのパターン多い
max, minの性質 †
- max(a, b)を、「aとbのどちらを選んでもよい」のように制約を緩和しても答えが一致するケースがある AGC28C
親関数 †
収束加速 †
- Aitkenがクソ早い
- ライプニッツ数列は1e10で収束だが、多重加速法を使うと長さ20くらいで収束する
順位・k番目 †
- K番目に小さいあたいを求めよ↓x 以下が K 個あるかを判定する問題にして x を二分探索
順位系をまとめる
http://abc062.contest.atcoder.jp/tasks/arc074_b
DynamicSumOfOrderK小さい方からk番目以内の合計(priority_queueのみ)
http://pekempey.hatenablog.com/entry/2016/05/16/235152
D-Query 永続
- BIT+二分探索でO(log n)で順位が可能らしい
- 数列aが与えられる。a[0:i]の上位k個の総和を全列挙せよ。
並列アルゴリズム †
- 並列ソート
- 奇遇転地法O(n)プロセッサでO(n)のソートアルゴリズム、確かにハードにあってそう。
- 理論的にはO(n log n)プロセッサでO(log n)ソートアルゴリズムがある。
マンハッタン距離 †
bit演算 †
- sumが限定のbitDP
- 和風いろはちゃん
- 1進数をconcatして持つと、sum bitになって持てるようになる
入出力 †
実験 †
- 極めて重要
- 天才みを感じたら即実験
- DPの高速化。以下を試す
- コストはmongeか?
- チョイスは縦に単調か?
- チョイスは横に単調か?
- DPテーブルは凸か?
フラクタル †
- フラクタルのn進数感(K分木になるので、どういうルートで言ったのかが後で辿れる)
- GCJ 2016 Qual D, yukicoder Fractal Gravity Glue
Simpath †
整数計画法 †
LP双対 †
概要 †
| 差分制約 | グラフ問題のポテンシャル差とみなすと、双対を取った時にグラフアルゴリズムが使えるようになることも | | 和の制約 | 無向アルゴリズムと対応する | | 最短経路 | 「p_i - c_e >= p_jの条件群を満たすp_t-p_sを最大化」が双対(牛ゲー) | | 最小費用流 | 「折れ線コストf(p_i-p_j)の線形和の最大最小」が双対 | | 最大流 | 最小カットが双対 | | 区間スケジューリング問題 | ABC103Dと双対 | | 連続ナップザック問題 | 双対取ると綺麗になるらしい |
- 用語
- 主LP=主問題(最大化・最小化するべき式)+主一般制約式+主変数制約
- 双対LP=双対問題(最大化・最小化するべき式)+双対一般制約式+双対変数制約
- 一般制約式は、変数の絡み合いを含む制約
- 変数制約は、x<=0, x>=0などの簡単なもの。
- ポテンシャル=主問題一般制約式に割り当てられた双対変数のこと(頂点制約だから頂点にたいする条件となる)
- 以下のもとで、主制約・双対制約の不等号の向きの変換は機械的にできる。
- 一般制約式の全ての不等号系が同じ
- 変数制約式の全ての不等号系が同じ
- そうではない場合は、適当に変数をおくとそのような形になる。
| 最小化問題 | 最大化問題 | | 変数x<=0 | 一般>= | | 変数制約なし | 一般= | | 変数x>=0 | 一般<= | | 一般<= | 変数x<=0 | | 一般= | 変数制約なし | | 一般>= | 変数x>=0 |
- LPを機械的に双対に変換する方法
- 主制約のそれぞれに、双対変数p_iを割り当てる
- 双対問題「min sum p_i [主制約の右辺]」が確定
- 主問題の係数ごとに、一本の双対制約が出る。以下を行う。
- 主問題の係数・変数のペア(c, x)を1つ固定する。c=0のものも。
- 双対制約の右辺=主問題係数
- 双対制約の左辺=全ての主一般制約s_iとそれに対応する双対変数p_iについて「s_iのxに関する係数 * p_i」を足したもの(要するに\( \sum_{p_i \in P} p_i \frac{\del s_i}{\del x} \))
- ポテンシャル
- 要するにグラフアルゴリズムをLPにした時の、主一般制約に対応する双対変数のこと。
限定分岐法 †
- f(x)を最小化sする時、xの確定した自由度Sと、確定していない自由度Tに分けて、f(x)=f(S, T)とすることを考える。
- 用語
- 許容解=下界=f(x)の今までに見つかった解の中で最も良い物
- (1)見つかり次第更新
- (2)貪欲関数b(x)を使って更新
- 緩和解=上界=f(x)の緩和問題g(x)の最適解(毎回計算する必要)
- 重要な性質
- 緩和問題が真の制約を満たすならば、それは厳密解(f(S, T)の中で、Tの最適解が確定する)
- 緩和<許容ならば、それは解になりえない(f(S, T)のTの全てが最適解を更新しない)
ll 許容解 = INF;
// 自由度sが確定していて、自由度tが未確定の時の最適解
ll dfs(state s, state t) {
緩和解 = g(s, t);
if (緩和解を与えるs, tが真の制約を満たす) return 許容解 = min(許容解, 緩和解);
if (緩和解>許容解) return INF;
ll ret = INF;
for (auto x : tの自由度のうち確定させたいものの集合) {
chmin(ret, dfs(s+x, t-x));
}
許容解 = min(許容解, 緩和解);
return ret;
}
int main(void) {
許容解 = 貪欲関数();
dfs(φ, all);
}
- 緩和関数の作り方
- ラグランジュ緩和=「条件に違反してる度」をminに突っ込む
min xy
s.t. x>0, y>0, x+y<1
min xy + s(x+y-1)
s.t. x>0, y>0
まとめるべきこと †
A*サーチ
要するに、ダイクストラでは今までの距離が短い順に展開していくが、A*では今までの距離+今からゴールまでのコストをが小さい順に展開していく。こういうことをすると、hの性質によっては最短距離が見つからなくなる可能性がある。しかし、hをノードnからゴールまでの距離だとした時、あるヒューリスティクス h(n) が 全てのノード n について 真のゴール距離 h*(n) を上回らない場合、hはAdmissible/許容的であると言う。こういう時のみ、A*による解は最適であることが保証される。
・サイクル列挙は全域木(サイクル基底を見ること)
最適路DAG †
- 最短路を実現するDAG
- 最短路を実現する経路のみで構成されたグラフ
- 最適な答えを出力するDPの答えとか
- DAGの数え上げやDPはトポソしなきゃ…とか思うくらいなら始点からメモ化再帰すればかんたん
高速ウオルシュ-アダマール変換 †
- SRM 518 div1 hard
- いつかのCSA
クエリ先読み †
BITとかで何か上手くできるやつ †
Mo †
永続の代用 †
- クエリ先読み+単調なデータ構造に対してできる永続の代替
- 単調=Incremental, Decrementalという意味
- パラレルバイナリサーチ
- Q個のクエリ先読み可能+クエリが時間に対して単調な場合、時間幅Tの永続データ構造に相当する機能を、省メモリでO((Q q+t)log T)で計算できる
ポテンシャル †
A*サーチが関係あるらしいので、A*を調べた。微妙に変なコストhを足しても最適解が保持されるようなヒューリスティック関数についての理論的考察。要するにh(n)=nからゴールに行くコストが真のコスト以下なら必ず最適解が保持される。(で、ポテンシャルってなんですか?)
Primal Dualは、fを流そうとする時の最小費用流O(FElogV)のアルゴリズム。かなりFord-Fulkersonに似ていて、残余グラフでDFSするかダイクストラするかという話(Ford Fulkersonは毎回DFSするのでO(fE)、Primal Dualは毎回ダイクストラするのでO(fElogV))
というか、Primal Dualってなんで負辺あるのにダイクストラできることになってるんですか
Primal Dualでなぜ負の辺があるのにダイクストラができるのか
負の辺があっても、実行可能ポテンシャルというやつが存在すればダイクストラ出来るひふ(それを最小費用流に応用したのがPrimal Dual)
http://www.bunkyo.ac.jp/~nemoto/lecture/shizu-sys1/shizu-shortestpath2003-r.pdf
http://d.hatena.ne.jp/smitch/20120305/1330926130
http://www.bunkyo.ac.jp/~nemoto/lecture/opt-model/2008/duality2-2006.pdf
LPとして見るとポテンシャルは双対変数で、グラフアルゴリズムとして見ると負辺を消すために導入する量ですね(直感的にはポテンシャルの値は原点からの最短路長で、この時辺のコストは「最短路よりどれくらい無駄か」みたいなものを表します)
簡約費用非負のポテンシャルを維持しながら可能流を求めているため。僕は下の本の3.3章で勉強しました。
amazon.co.jp/Text-数理最適化-久野-誉人/dp/4274212440
全点対最短路のJhonsonは非負維持じゃなくて非負化にポテンシャルを使っていて面白い。(この動画が分かりやすい→youtube.com/watch?v=NzgFUw…)LPの頂点の双対変数がポテンシャルらしいけどよく分からない。
緩和問題のLPとやらは結構一般生がありそうだし実装パターンを得たい気持ち
http://ci.nii.ac.jp/naid/110002768734
セグ木に平衡二分木をのせる †
- segment [i, j) = 「x[i, j))の区間に含まれる(x, y)のyを全て管理するordered set」などとする
- 動的にrangefreqやrangesumを行えるようになる
- quantileはO(log^2 n log amax)などでできる
- segment [i, j) = 「x[i, j)に含まれる全ての点群のy座標」
b+木 †
フラクショナルカスケーディング †
最良計算量・コード量チャレンジ †
- 順方向から読むケースと逆方向から読むケースがあったら、別にreverseをする必要はない。
- とりまソートはやめる
- 範囲指定とかならそのまま範囲指定のifを入れれば良いだけ
点と直線の双対関係 †
分数不等式の最大最小 †
- lgauss(a, b), ugauss(a, b) を分数 a / b の切り下げ切り上げ関数として、
- n<a/bなる最大のnはlgauss(a-1, b)
- n>a/bなる最小のnはugauss(a+1, b)
- n<=a/bなる最大のnはlgauss(a, b)
- n>=a/bなる最小のnはugauss(a, b)
setとmapを管理する実装 †
- set系内部でeraseしたり云々したりする場合はfor (auto x : s)とかfor (auto it = begin(s); it != end(s); it++) とかしないで、while (s.empty())なりwhile(1)するなりすること!
- setやmapにはfindというメソッドがあって、これを使うとイテレータを得ることができる
- lower_boundで得るのではなく、findで得るべき。
- multisetでは、erase(値)ではなくerase(iterator)で削除しないと全要素が消えてしまう。
- setとmapのeraseには[from, to)のイテレータを指定するモードがあって、便利っぽい
- iteratorは(1)取得(2)++(3)削除の順番でやる、というのはもう頭に入れとけば良いと思う
線形代数 †
- 競プロにおける線形代数,行列ももちろんだけど行基本変形するやつとか基底求めて最小化するやつとかSRMdiv1medあたりでたまに見る気がする
- 2017 DDCC本戦か何かの、xorのベクトルの独立成分を見るやつがあったはず
最小・最大問題の特徴 †
- 辺のコストがmin(A, B)だったらA,Bの二辺を張るのは典型
- 二分探索
多倍長演算 †
- 多倍長演算を木構造的に管理すると、n桁とm桁の乗算がO(n m)なのに、多倍長整数N個全体かけるのにO(N^2)しかかからない
- 多倍長演算を高速に行うアルゴリズム
- 愚直
- カラツバ\( O(n^{1.585}) \)
- The Schönhage–Strassen algorithm \( O(n \log n \log \log n) \)
- 更に早いFürer's algorithmもあるが微々たるもの
不明瞭要求 †
- 「最大値を与えるインデックスを教えてください」
- 何個か不定!0個の可能性もあるし、2個以上の可能性もある。
|
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)
![[PukiWiki] [PukiWiki]](image/pukiwiki.png)